Planetenbahnen

Wie sich Planeten um die Sonne oder Satelliten um die Erde bewegen, lässt sich berechnen, das ist aber nicht ganz einfach. Als ich im Jahr 1985 meinen ersten Home-Computer hatte – einen C64 – habe ich als Programmier-Übung und Spielerei versucht, die Bahnkurve eines Planeten im Schwerefeld der Sonne numerisch berechnen zu lassen. Zunächst mit einem BASIC-Programm, das quälend langsam lief, dann als Assembler-Code, das ging schneller, die ersten Ergebnisse waren aber enttäuschend.

Später, als ich Bilder für meine Webseiten erstellte, wo es auf genaue Farbwiedergabe ankam, habe ich mich mit der Programmier- und Seitenbeschreibungssprache PostScript angefreundet und dann, wieder als kleine Übung, noch einmal die numerische Simulation der Planetenbahnen aufgegriffen. Das ist auch schon einige Jahre her.

Um zu zeigen, dass es heute leicht ist, das Kepler-Problem auf dem Computer zu veranschaulichen, stelle ich das kleine Programm mit einigen Ergebnissen hier vor. Was man braucht, um PostScript auf dem PC auszuführen, habe ich an anderer Stelle beschrieben.

Betrachtet wird die Bewegung eines Massenpunktes in der Ebene unter Einfluss der vom Zentrum im Koordinatenursprung ausgehenden Gravitationskraft. Länge und Zeit werden in willkürlichen Einheiten gemessen und die Masse des Planeten bzw. Satelliten sei 1. Die Newtonsche Bewegungsgleichung „ Kraft = Masse × Beschleunigung “ gilt für die x- und die y-Koordinate getrennt.

Der Betrag der Gravitationskraft ist proportional zu 1/r², wobei r der Abstand vom Zentrum ist, also r = √x²+y². Daraus ergibt sich für die x- und y-Komponente der Kraft

F_x(x,y) = − κ x /(x²+y²)^3/2, F_y(x,y) = − κ y /(x²+y²)^3/2,

Zur Zeit t = 0 soll der Satellit sich am Ort x₀, y₀ befinden und die Geschwindigkeit v_x,0, v_y,0 haben. Einen winzigen Zeitabschnitt h später befindet er sich am Ort x₁, y₁ und hat die Geschwindigkeit v_x,1, v_y,1. Da sich die Geschwindigkeit über diesen Zeitraum nur ganz wenig ändert, gilt in guter Näherung

v_x,1 ≈ v_x,0 + F_x(x₀,y₀) h, v_y,1 ≈ v_y,0 + F_y(x₀,y₀) h.

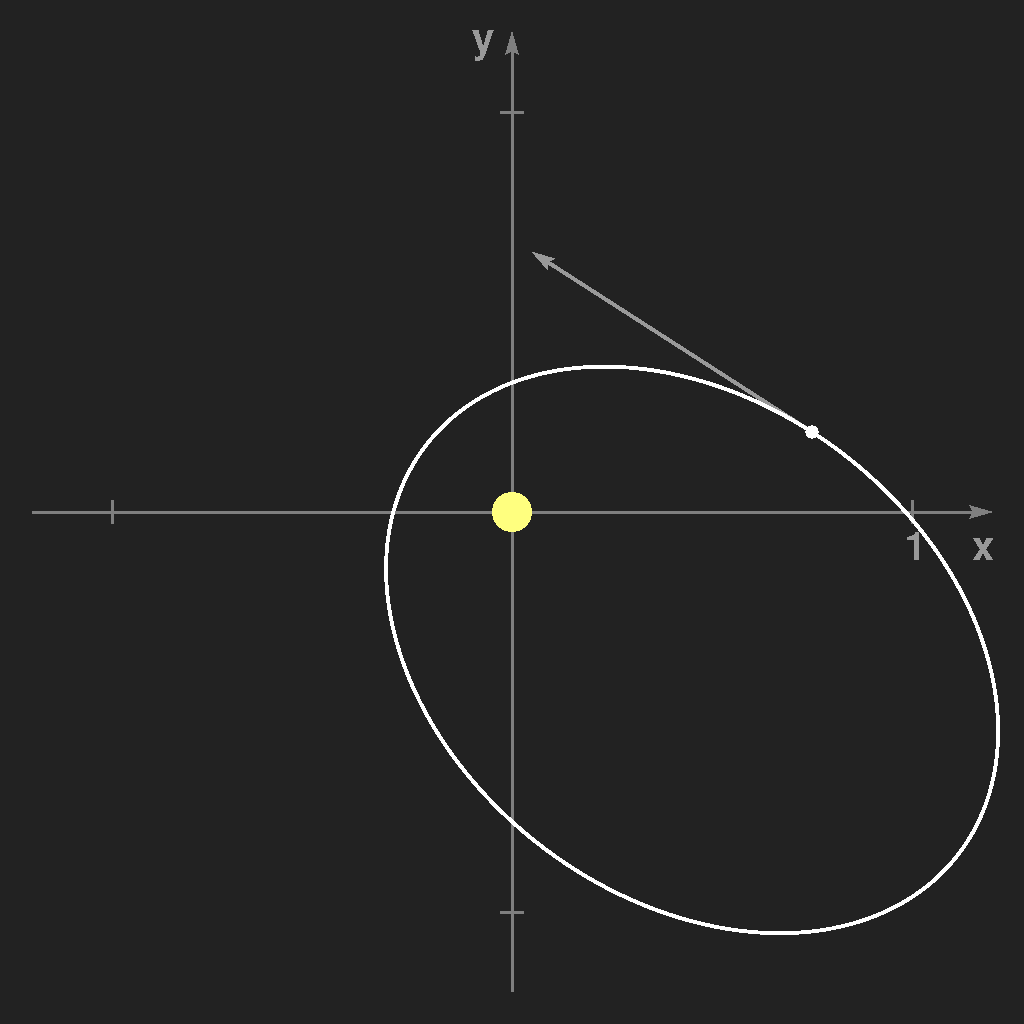
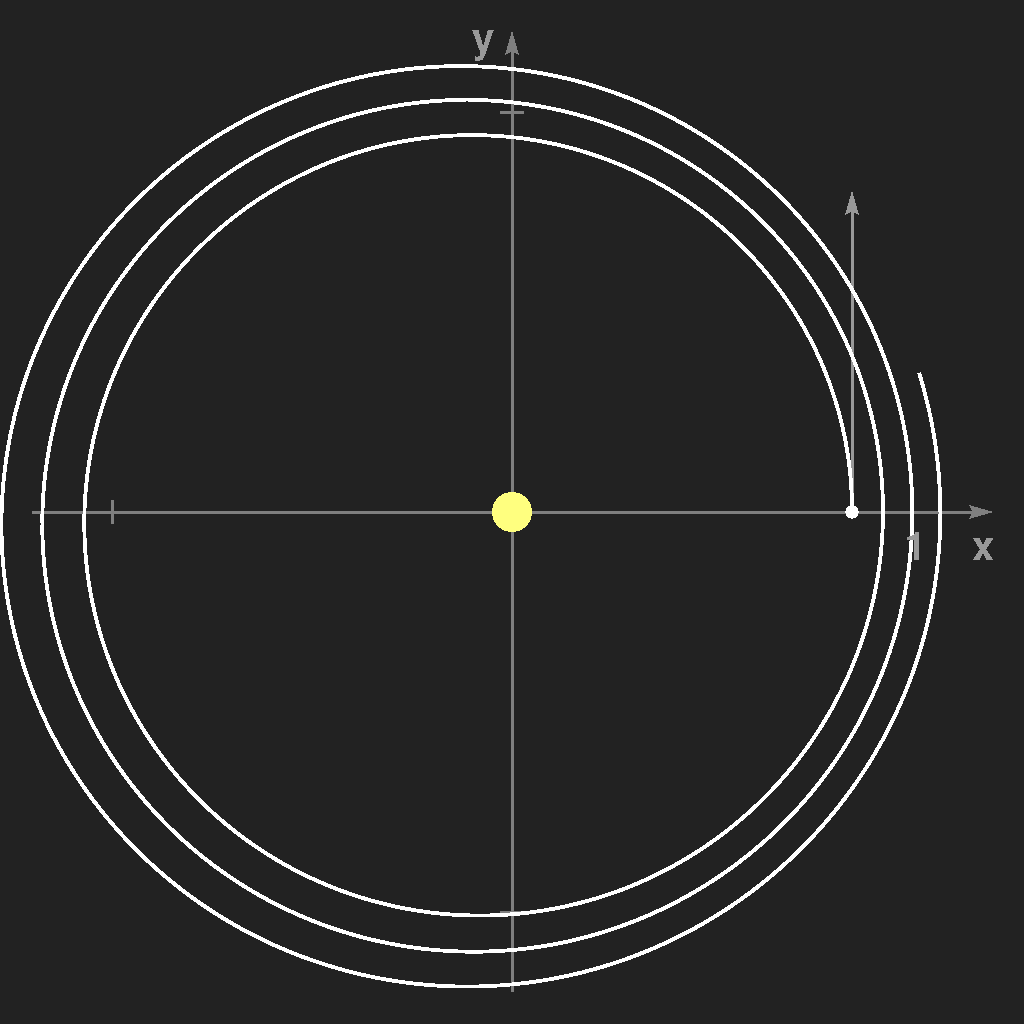
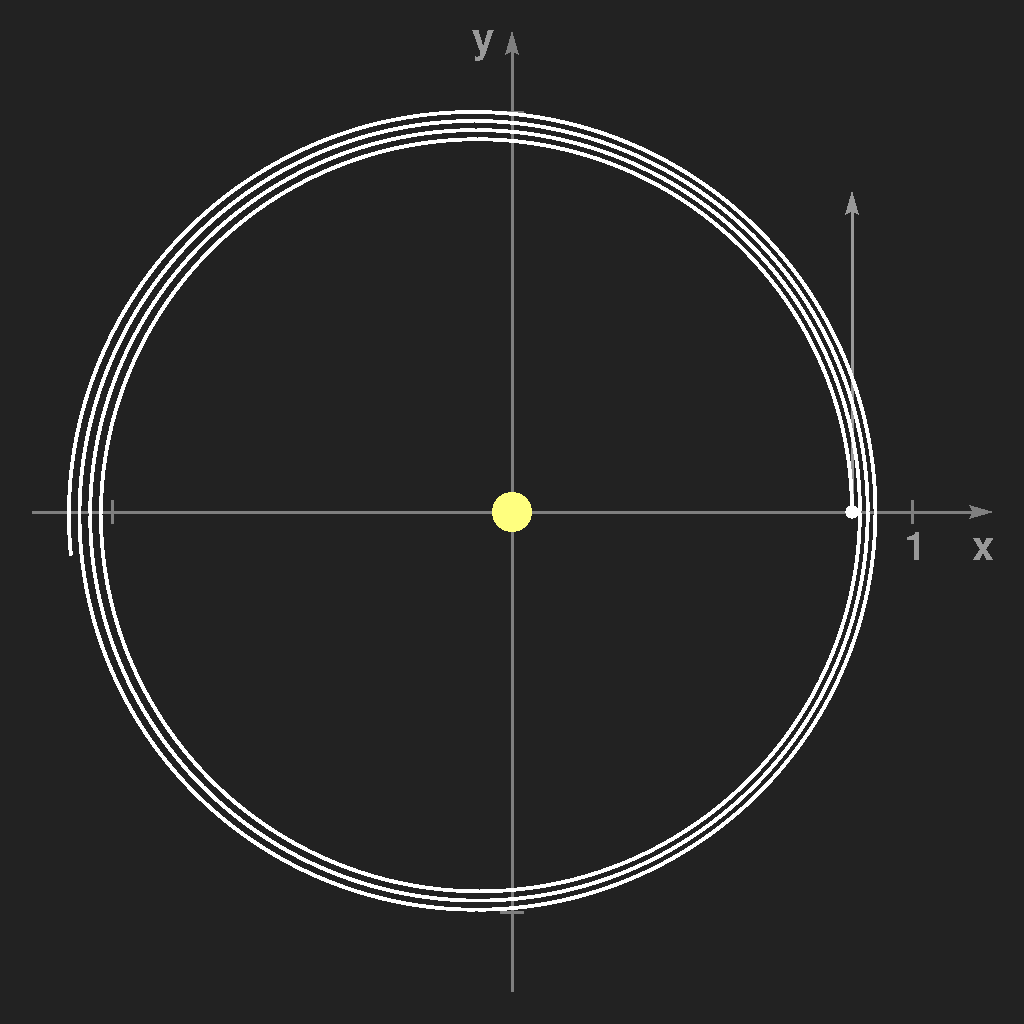
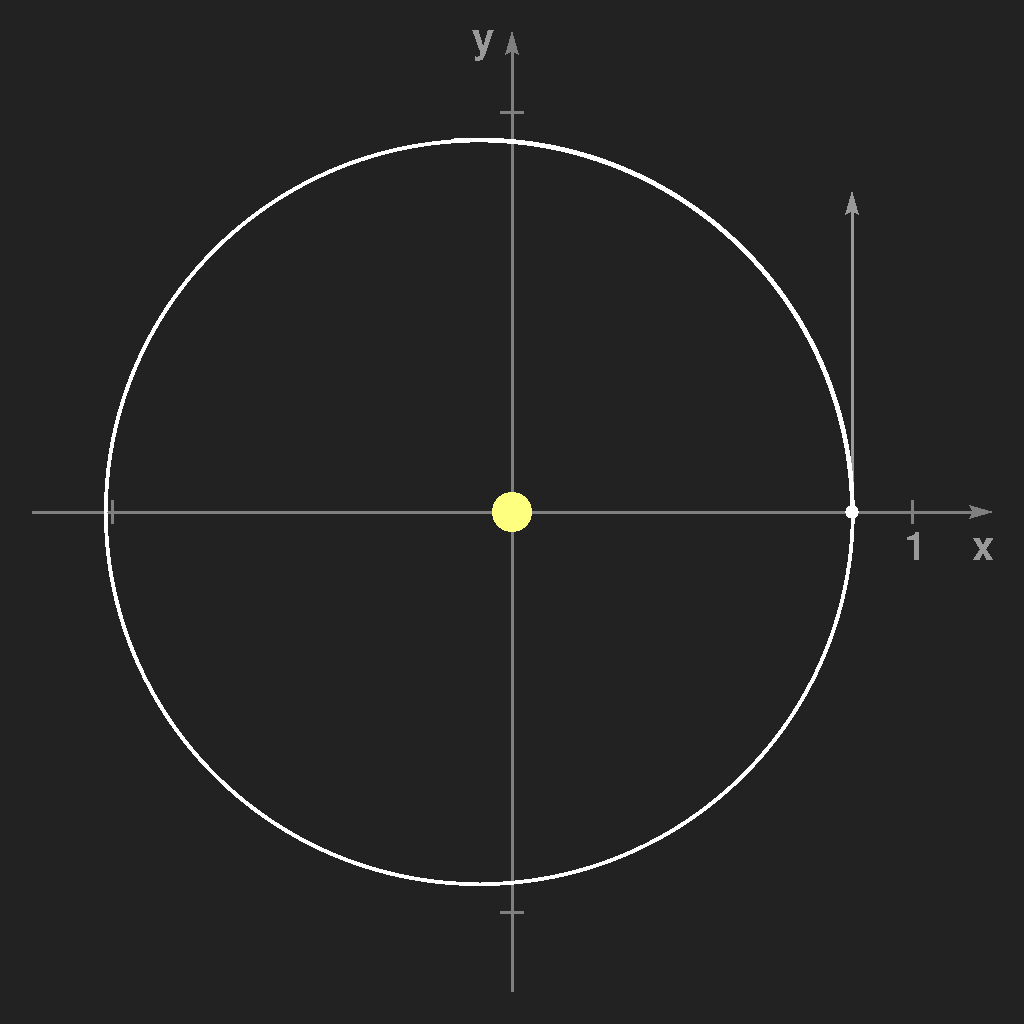
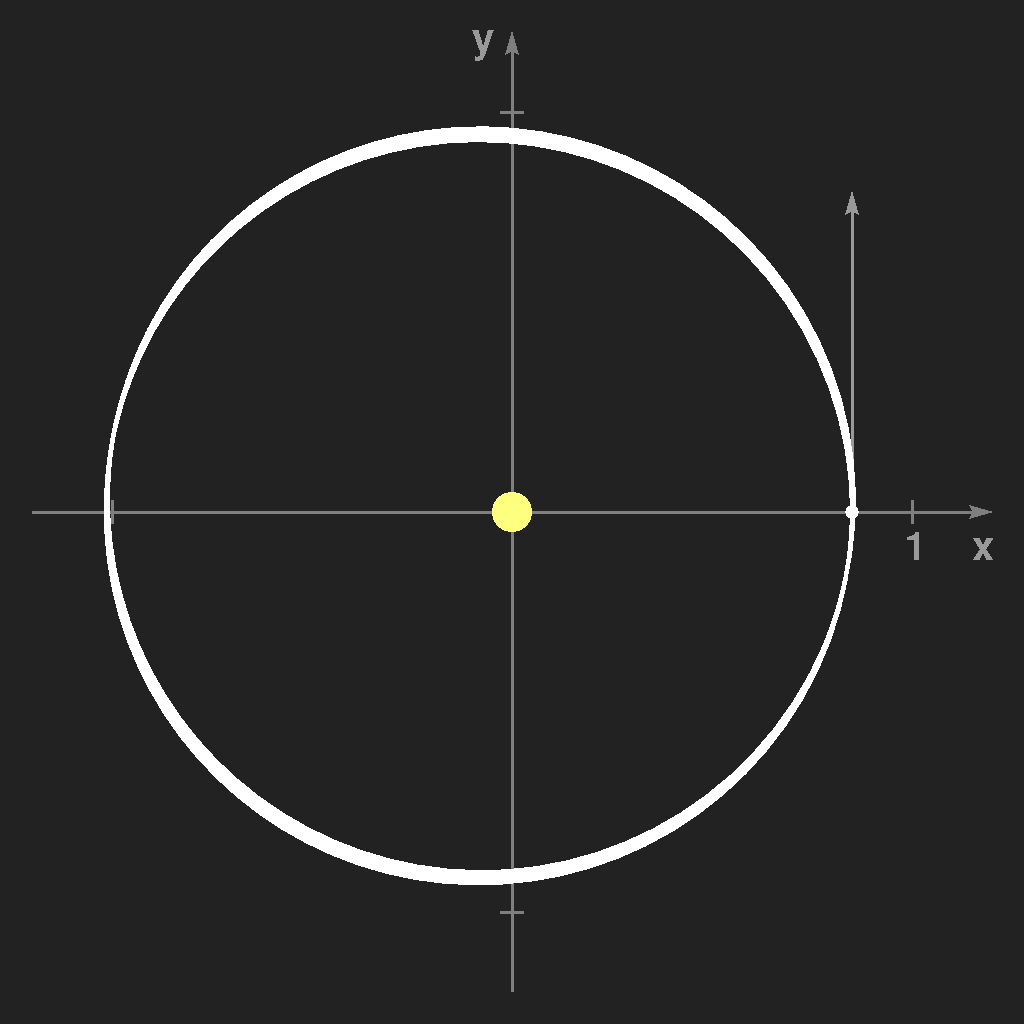
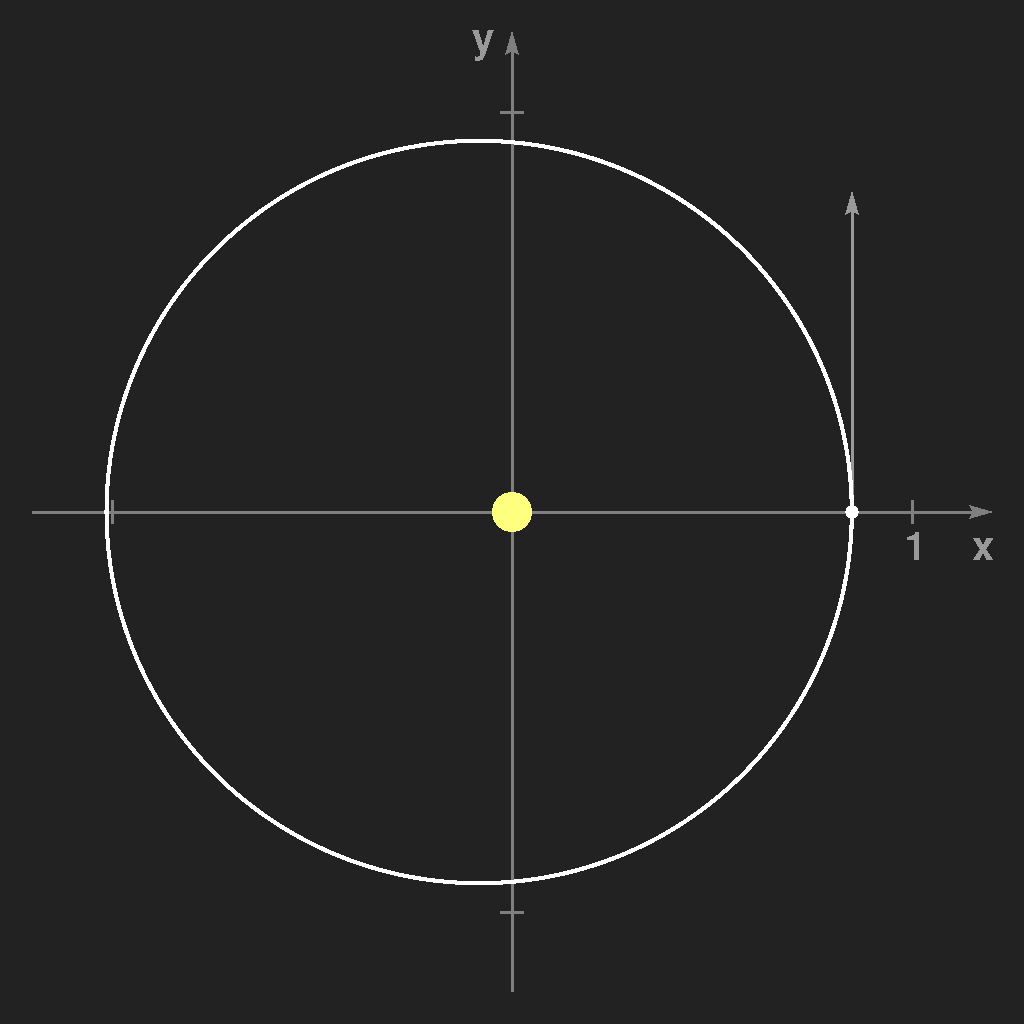
Dann wählt man den soeben errechneten Punkt als neuen Ausgangspunkt für das nächste Zeitintervall h, d.h. man ersetzt x₀ durch x₁ etc. und wiederholt das Ganze immer wieder. Ergebnisse dieses Verfahrens sind in den folgenden Bildern zu sehen:

Der Anfangspunkt ist markiert; der von diesem Punkt nach oben zeigende Pfeil gibt die Anfangsgeschwindigkeit an, also die Strecke, die der Satellit in einer Zeiteinheit zurücklegen würde, wenn keine Kraft auf ihn einwirkte. Im linken Bild ist das kleine Zeitintervall h = 0.01, im mittleren Bild ist h = 0.0025 und im rechten 0.00025 Zeiteinheiten.

Man sieht, dass h sehr klein gewählt werden muss, um ausreichende Genauigkeit zu erreichen. Dies ist nicht sehr befriedigend, aber man kann es besser machen. Man betrachtet den Zeitpunkt t = h / 2 und rechnet für diesen Punkt die Geschwindigkeit und die Beschleunigung (= die Kraft) aus. Diese beiden Werte sind eine sehr gute Näherung der mittleren Geschwindigkeit und mittleren Beschleunigung in diesem Intervall, und mit diesen Werten berechnet man dann den Ort und die Geschwindigkeit zur Zeit h, den Ausgangspunkt für die nächste Wiederholung des Verfahrens.

Und schließlich geht es noch genauer. Es liegt ja ein System von vier gekoppelten Differentialgleichungen erster Ordnung vor:

das nach dem Runge-Kutta-Verfahren numerisch integriert werden kann, worauf ich hier aber nicht näher eingehen will.

Links: verbesserte Näherung wie oben beschrieben, rechts: Runge-Kutta-Näherung. Die Schrittweite ist in beiden Fällen relativ groß, h = 0.1, und es wurden 3000 Iterationsschritte durchgeführt, was ca. 35 Umläufen entspricht.

Das Programm kann hier heruntergeladen werden: Planet.eps. Die Zahlen in den Zeilen 7 bis 15 können mit Hilfe des Editors (auf jedem Rechner vorhanden) verändert werden, um andere Bahnkurven zu sehen. Hier nur ein Beispiel:

Planeten- und Satellitenbahnen