Erläuterungen zur Kritik an Küppers' Farbenlehre von D. Zawischa
Ein didaktisches Utopia
Meine Perspektive ist die des Experten für Bildreproduktion, für Mehrfarbendruck, für Mischprozesse von Farbmitteln und für didaktische Farbenlehre
behauptet Küppers von sich.
|
Nehmen wir jetzt einmal an, die Grundempfindungskurven sähen so aus, wie in nebenstehendem Bild gezeigt.
Wenn nur die für lange Wellenlängen des Lichtes empfindlichen Zapfen angeregt werden, entsteht die Grundempfindung Rot, die wir auch, um sie von Purpurrot zu unterscheiden, nach Goethe Gelbrot nennen können. Diese Urfarbe lässt sich durch jeden Farbreiz, dessen Wellenlängen alle größer als 615 nm sind, hervorrufen. Entsprechend wird durch Licht mit allen enthaltenen Wellenlängen kürzer als 385 nm die Urfarbe Violettblau hervorgerufen, denn es werden nur die für die kurzen Wellenlängen empfindlichen Zapfen angeregt. |
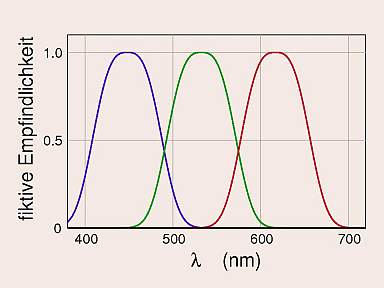 |
Die Grundempfindung und Urfarbe Grün ließe sich durch einen schmalbandigen Farbreiz mit Wellenlängen etwa zwischen 525 und 540 nm verwirklichen.
|
Alle möglichen Farben lassen sich als Summen von Teilmengen aus diesen Urfarben deuten und auch realisieren. Als Ordnungssystem bietet sich an, die Farben als Vektoren ("Pfeile") in einem dreidimensionalen Raum darzustellen. Man unterscheidet zwischen Farbart und Helligkei; die Helligkeit ist durch die Länge dieser Vektorpfeile bestimmt und die Farbart durch ihre Richtung. Und wenn man sich nur für die Farbart interessiert, dann kann man die Richtung durch die Durchstoßpunkte dieser Vektorpfeile durch die Einheitsebene r + g + b = 1 angeben und man erhält auf diese Weise für die Darstellung aller Farbarten das Farbendreieck. Färbt man die Durchstoßpunkte mit den zugehörigen Farben in maximaler Helligkeit ein, so erhält man das Bild, das rechts zu sehen ist. |
 |
Die Farben in der Illustration sind natürlich nur annähernd richtig wiedergegeben, weil wir ja nicht in Utopia sind; aber es ist festzuhalten, dass alle möglichen Farbarten in dem Dreieck enthalten sind. Es müssen daher auch die Spektralfarben da sein. Wo sind die?
Die Antwort ist ganz einfach, man kann sie aus dem Bild mit den Empfindlichkeitskurven ablesen: alle Wellenlängen unter 450 nm finden sich in der linken unteren Ecke des Dreiecks, dann geht es entlang der linken Seite nach oben, in der Mitte der Seite, bei der Farbe Cyan, ist die Wellenlänge 490 nm, an der oberen Ecke, bei der Urfarbe Grün, 532.5 nm, und dann geht es auf der rechten Seite wieder abwärts, 575 nm sind es bei Gelb
und bei 615 nm wird die rechte untere Ecke erreicht, wo sich auch alle Wellenlängen größer als 615 nm befinden. Wenn Sie den Mauszeiger über das Bild führen, sehen Sie den Spektralfarbenzug eingezeichnet.
Zurück zur Wirklichkeit
Nun ist seit den dreißiger Jahren des 20.Jahrhunderts schon bekannt, wie die Grundempfindungskurven des menschlichen Auges aussehen (in dem an anderer Stelle schon einmal gezeigten
Bild sind sie so normiert, dass die Fläche unter allen drei Kurven gleich ist, im folgenden ebenfalls, aber in beiden Fällen in willkürlichen Einheiten).
|
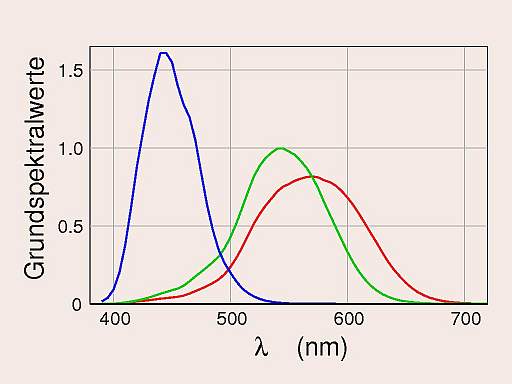
Seit damals sind viele neue experimentelle Daten hinzugekommen. Rechts sind die Empfindlichkeitskurven zu sehen, die im Jahr 2000 von Stockman und Sharpe publiziert wurden; die Daten findet man auf den Internetseiten des Colour & Vision Research Laboratory des UCL (University College London) unter dem Stichwort "cone fundamentals". |
 |
|
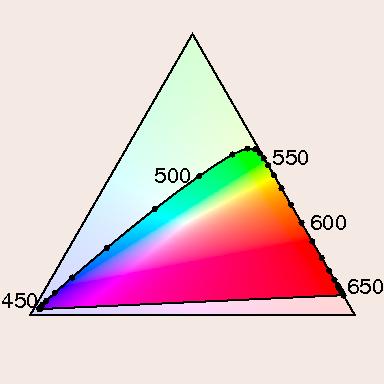
Den Empfindlichkeitskurven kann man entnehmen, dass es möglich ist, die L-Zapfen allein anzuregen, wenn man Licht einer Wellenlänge verwendet, die größer ist als 650 nm. Um nur die S-Zapfen anzuregen braucht man Licht vom kurzwelligen Ende des Spektrums; bei einer Wellenlänge von 436 nm, wie sie für colorimetrische Messungen verwendet wird, werden die M- und L-Zapfen nur sehr wenig angeregt, hier kommt man der Zapfen-Primärvalenz zumindest recht nahe. Aber eine Lichtquelle, die nur die M-Zapfen anregt und die anderen nicht, die gibt es nicht. Wählen wir spektralreines Licht mit der Wellenlänge 520 nm und versuchen jetzt alle möglichen additiven Mischungen (wieder mit größtmöglicher Helligkeit). Das Ergebnis ist rechts zu sehen. | |
 |
Es sieht genau so aus wie das utopische Farbdreieck weiter oben, weil auch hier die Einfärbung nur schematisch erfolgt ist, da am Bildschirm nicht die richtigen Spektralfarben zur Verfügung stehen. Aber es gibt einen wesentlichen Unterschied: mit den drei gewählten Primärvalenzen lassen sich die anderen Spektralfarben nicht mehr durch Überlagerung (additive Mischung) erzielen. Der Spektralfarbenzug (der geometrische Ort aller Spektralfarben) berührt das Dreieck nur an den Eckpunkten und liegt ansonsten außerhalb. Das liegt daran, dass die gewählte Grün-Primärvalenz nicht nur die M-Zapfen anregt, sondern die L-Zapfen ebenfalls noch deutlich und die S-Zapfen auch noch ein wenig. Um z.B. das Grün bei 500 nm zu reproduzieren, müsste man die Anregung der L-Zapfen reduzieren, man bräuchte "negatives Rotlicht".
Aber wie sähe das Farbdreieck aus, wenn man sich den Farbraum von den Zapfen-Primärvalenzen aufgespannt denkt? Experimentell lässt sich dies nicht bewerkstelligen, aber berechnen schon, siehe das Bild rechts. Wenn Sie den Mauszeiger in die Nähe des Bildes bringen, dann werden alle Farben, die sich auf einem sRGB-Bildschirm nicht exakt wiedergeben lassen, ausgeblendet.
Alle irgendwie durch physikalische Farbreize hervorrufbaren Farbarten liegen innerhalb des vom Spektralfarbenzug gebildeten Bogens, den man zur Verdeutlichung dieses Sachverhalts gerne durch die Sehne der "Purpurgeraden" abschließt.
| |
|
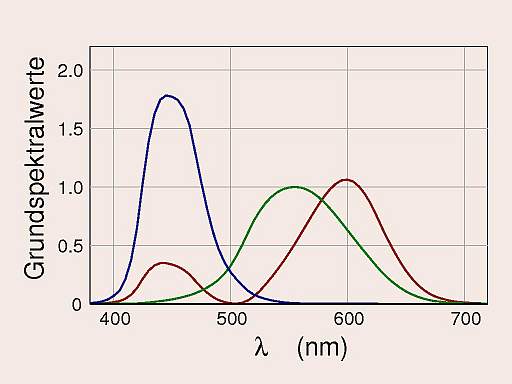
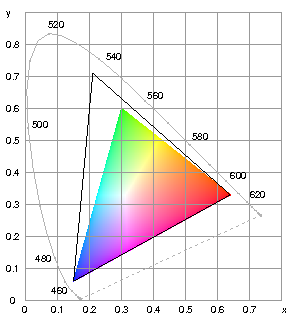
Eine solide Grundlage für die Farbmetrik wurde 1931 von der Internationalen Beleuchtungskommission (CIE, Commission Internationale de l'Eclairage) durch die Einführung des Normalbeobachters geschaffen. Dessen "Grundempfindungskurven" ‾xλ, ‾yλ und ‾zλ – Überlagerungen aus den experimentell ermittelten Spektralwertkurven (Farbvergleichskurven) – wurden so gewählt, dass den Farbreizen X ("virtuelles Rot") und Z ("virtuelles Blau") keine Helligkeit zukommt, die Helligkeit allein von Y ("virtuelles Grün") beigesteuert wird.
 |
|
| Die Normspektralwertkurven (CIE1931), die man als Empfindlichkeitskurven des fiktiven Normalbeobachters interpretieren kann. | Das CIE-x-y-Diagramm mit Spektralfarbenzug, Purpurgerade und einem
Vergleich zweier Farbbereiche: sRGB (bunt) und Adobe-RGB (1998) (ausgezogenes Dreieck). (Siehe auch Farbe für den Bildschirm".) |
Üblicherweise wird das sich ergebende Farbdreieck als rechtwinkeliges Dreieck gezeichnet, wobei auch noch die leeren Ecken abgeschnitten werden – so entsteht die Normfarbtafel, das CIE-x-y-Diagramm.
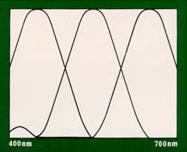
Küppers zieht es vor, die experimentellen Daten zu ignorieren und präsentiert stattdessen immer wieder die grob verfälschten und von ihm vermuteten Zapfenempfindlichkeitskurven.
| |  |
|
"Die Kurven [...] sind ein grobes Schema der Spektralwertkurven, wie sie vermutlich in ähnlicher Weise bei einem farbentüchtigen Normalmenschen vorhanden sind" |
|
Küppers' Unbuntart-Sechseck (hier mit der Unbuntart Weiß) mit den sechs bunten Grundfarben an den Ecken, "das Farbensechseck mit der logischen quantitativen Ordnung der bunten Farben". |
Küppers kommt durch "stringente Logik" zu dem Schluss, dass der Farbraum, der alle möglichen Farbempfindungen enthält, von ebenen Flächen begrenzt ist und sich am besten in der Form eines Rhomboeders darstellen lässt. Dies wird durch die Krümmung des Spektralfarbenzuges widerlegt. Wenn man im Vektormodell des Farbraumes den Raumanteil ermittelt, der von allen nur denkbaren Oberflächenfarben erfüllt ist, so ergibt sich ein von gekrümmten Flächen begrenzter Körper (Bild unten), kein Würfel, kein Rhomboeder und kein Parallelepiped.
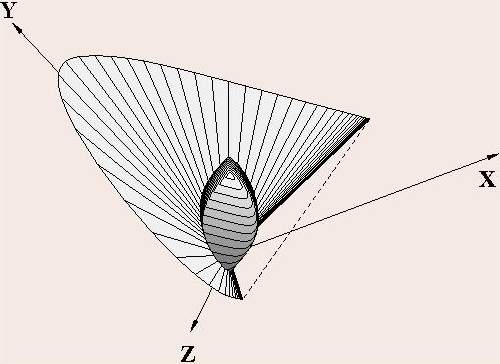
Küppers geht von seinen Erfahrungen im Drei- oder Vierfarbendruck aus und überträgt diese einfach auf die Farbempfindungen. In seinen Farbatlanten tauchen gedruckte Farben mit den Bezeichnungen C99, M99 und Y99 auf, diese stehen andererseits für die jeweiligen extremen Farbempfindungen, er tut also so, als ob man diese durch Druckfarben auf Papier hervorrufen könnte. Er setzt standardisierte Beleuchtungs- und Beobachtungsbedingungen voraus, aber auch dann ist das Rhomboeder nur eine Veranschaulichung der im Druck mit den Farben Cyan, Magenta und Gelb (Y) erzielbaren Farben (beziehungsweise der mit acht Farbpigmenten erzielbaren) und nicht der Raum aller möglichen Farbempfindungen.
Zurück zum Text oder zur Übersicht.











