Quetelet rings

Quetelet rings may be not very rare, but until now I have only seen artificially produced ones. Impressive examples due to dust particles or algae on the surface of a pond or puddle may be found in the web [1], [2],[3], [4].

Recently Aleksandr Berdnikov uploaded three photographs of a dusty mirror which show this phenomenon very clearly:

The images (source: Wikimedia Commons [A], [B], [C]) have been taken with lhe light source closer to the mirror than the camera (about half as far, left image), with the flashlight twice as far as the camera (middle), and with camera and light approximately at the same distance (right).

Aleksandr in his comments to the images describes the relative positions of the flashlight to the camera; but this can be deduced from the images, if only the relative distances are known. In the right picture, the mirror images of the light source and the camera are visible, therefore the arrangement is clear. The other two photos show only the flashlight mirrored. But the dark area in the lower right corner of the first picture must be the back of the light, thus it is to the right and lower than the camera, while in the second picture there certainly it is the shadow of the camera which obscures part of the lower right, which means that the light is to the left and higher up. There are some reflections of the surroundings in this shadow and below. (Click on the pictures to enlarge!)

As seen on the photographs, the rings are circular, but unlike coronas or aureoles they are not centred around the light source.

   
  

I first deal with the case (which I haven't yet seen) of algae like Chromulina rosanoffii over a calm water surface. As shown by Marko Riikonen [4] “this unique sort of alga separates itself from the water surface by forming a stalk on top of which it rests”.

The colours are due to the interference of light rays coming from the same point of the source and arriving at the same point of the retina (or the camera's sensor), but having travelled different paths. The two interfering beams are: light, which is reflected at the water surface and is afterwards scattered to the observer by the particle (an alga), the black line in the neighbouting sketch, and light which first is scattered by a particle, then is reflected by the water surface and finally reaches the observer (white line).

The sketch to the right is not to scale, actually the particle (white circle) and its mirror image (light grey circle) are so close together that they cannot be resolved by the eye (or camera).

Knowing that the rings are concentric circles (I shall show this later), it is not difficult to find the position of the centre. Consider the brightest circle which goes through the mirror image of the sun, which is the locus of all points where the two paths have the same length. Another easily to locate point on this circle is the antisolar point in the shadow of one's head. The centre of the rings is just halfway between the antisolar point and the image of the sun, and this is just under the feet of the observer, the nadir.

This is not the case if the light source is close, comparable with the distance of the observer from the mirror. Instead of the antisolar point now the point has to be considered which is just hidden by the lamp (B in the adjacent sketch) or where the shadow of the observer's eye would be (B in the rightmost sketch). If produced by dust on a mirror, the rings are only seen if the illumination angle and viewing angle (as measured from the normal) are small. The pair of sketches to the right illustrates how to find the centre of the rings in this case, and they also illustrate that the rings on the mirror are not changed when the positions of observer and lamp are exchanged.

The three photos below have been taken with a small circular mirror with 11 cm diameter. For the left and middle one, a small incandescent lamp was positioned approximately 5 m far from it, and the camera at about half that distance. These two images differ only in focusing: the rings get more pronounced if the light source is in focus, not the grains on the glass.

The third photograph below has been taken with the camera at 2.5 m and the lamp at 80 cm effective distance. A glass plate has been used to reflect its light to the mirror, therefore “point B” is not obscured by the lamp's case.

Circles on water

   

To show that the coloured rings are circular, I first treat the simpler case where the sun is the light source. Let the z-axis point upwards, the x-axis to the left and the y-axis towards you. Let the origin be at the height of the water surface and the eye of the observer at x=y=0, z=a.

Until they reach the yellow line in the neighbouring sketch, the “black” and the “white” ray have travelled the same length. The black path from the yellow line to the water and then up to the particle has the length s₁. After being scattered by the particle, the length of the white ray is the same as if it came from the particle's mirror image. After the rightmost yellow line, the length of the black line and that of the white path (dashed in the beginning) is the same again. Thus, the path length difference of the two beams is just Δ = s₁−s₂.

From the drawing we have s₁=2d cos(θ), and, as the eye is much farther than shown in the not-to-scale drawing, the rays to the eye may be assumed to be parallel and we get s₂=2d cos(α). Thus,

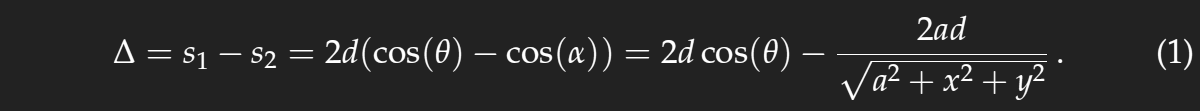
The path length difference Δ determines the colour. Looking for the ring of a certain colour, we choose the corresponding value of Δ and obtain after a little agebra

what is the equation of a circle centred at the base point of the observer, as stated before.

   

Circles on mirrors

Now consider a lamp at a distance of only few meters and a dusted mirror instead of a pond or puddle. The geometry is different as the dust particles are quite far from the silvery back side of the mirror (2 to 3 mm), and therefore interference fringes can only be seen at very small angles α and β. The rays are refracted by the glass; instead of the angles α and β, in the glass we have α' and β' which are determined by Snell's law. As the angles are very small, we can approximate sin(α) by α etc. and get

where n is the refractive index of the glass. From the sketches to the right we see that

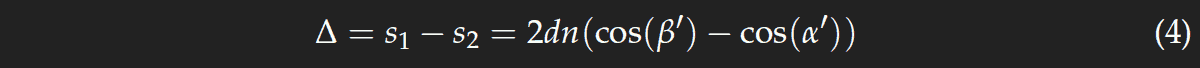
There is an additional factor n, because the optical path length and not the geometric length has to be taken. Making use of eq. (3), and cos²(x)=1−sin²(x), we get

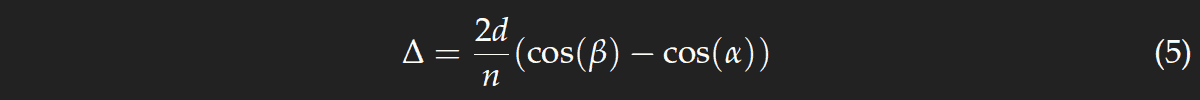
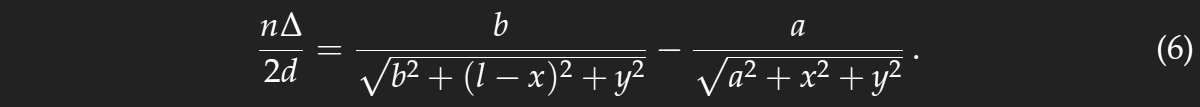
Now the distances a and b are much larger than the distance l and the values of the coordinates x and y which are of interest, and as expressions like (1+x)^−1/2 can be approximated by 1−x/2 if |x|<<1, we get

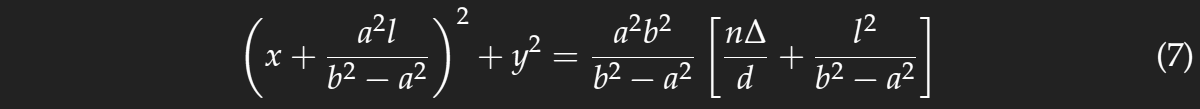
– a circle centred at neither the mirror image of the lamp nor that of the observer's eye. The centre is independent of Δ, therefore the rings are concentric circles.

Back to the index page "the origins of colour"