|
|
| Photo © Mathias Müller (site), shown with permission |
The above photograph, a view of Hannover at night, aroused my curiosity because of the beautiful stars around the street lamps.
The stars are certainly diffraction effects due to the shape of the camera's aperture. To demonstrate that, I computed the images of a point-like, monochromatic light source for a variety of shapes, the figures just below show results for a seven-bladed aperture diaphragm. For the photograph above, the focal lengts was f = 42 mm, and the aperture was f/32. I used those values and the wavelength of λ = 555 nm.




The first image in the row shows a pattern which looks very much like the Airy disk of a circular aperture. The width of the image corresponds to 0.2 mm on the sensor of the camera. The brightness of the consecutive diffraction rings falls off very rapidly and no starlike shape is seen. This changes if the brightness is increased so that the central spot is severely overexposed, as shown in the next figures, the widths of which is now 2 mm. In the first, second, and fourth figure, the light source is in focus while in the third one some defocussing is simulated. The last image differs from the second one in that the blades of the diaphragm are slightly curved.
In the spikes of the stars interference causes alternating light and dark regions. These are never seen in this clarity on real photographs for two reasons. Firstly, most light sources are not point-like, they have a finite extension which blurs the image, and secondly, they emit light which is a composition of many different wavelengths, while the computation was done with a fixed wavelength (monochromatic light).
I took two pictures of a nightly scene in a more rural region, one with aperture f/8, the other one with f/3.2, which is the widest opening at the given focal length. Clearly, the star-like appearance of the street lights is due to the shape of the aperture of the diaphragm which in this case is a hexagon formed by six slightly curved blades.


Below some more computer-generated pictures are shown which illustrate the influence of the diaphragm on the image of a point-like monochromatic light source. (For better visibility, grey-scale images instead of green ones are presented.) The following parameters have been used: wavelength λ = 555 nm, aperture D = f/8, focal length f = 10 mm.
Click to enlarge!



Left: Hexagonal aperture, image width 0.06 mm. No overexposure of the central spot.
Middle: The same hexagonal aperture, image width 0.6 mm, central spot overexposed 3000 times.
Right: Hexagonal aperture formed by slightly curved blades, overexposed 3000 times
It is seen that the curvature of the edges leads to diffusely ending prongs of the stars.
Assume that a nearly point-like light source is in focus. For the computation, the geometry is slightly idealized. We assume that the objective consists of two ideal thin lenses, one in front of the diaphragm, the other behind it. Their focal lengths are chosen such that plane waves are passing the aperture. Then, instead of Fresnel diffraction, we may consider the simpler Fraunhofer diffraction to obtain the image on the camera's sensor or film.
Though there probably are no cameras with quadratic aperture, let us first consider just this case because of its simplicity.
The diffraction pattern of a square hole in a diaphragm is the same as that of two crossed slits. Therefore, knowing the intensity distribution generated by a single slit we also know that caused by a sqare aperture.
As the width of the slit, a, is always very much larger than the wavelength λ, the sine of the deflection angle may be replaced by the angle (in radians) or by its tangent. Assuming that behind the slit a lens focuses the pattern on a screen, sin(α) may thus be replaced by x ⁄ f, where x is the distance from the central maximum measured on the screen, and f is the focal length of the lens.
To compute the amplitude of the diffracted wave for any angle, one has to perform the summation (integration) over the width of the slit. The corresponding mathematics may be found in Wikipedia.
The normalized amplitude and the normalized intensity of the diffracted wave are given by
The next figure shows the amplitude (blue-green), the intensity (white) and hundred times the intensity (dark red).
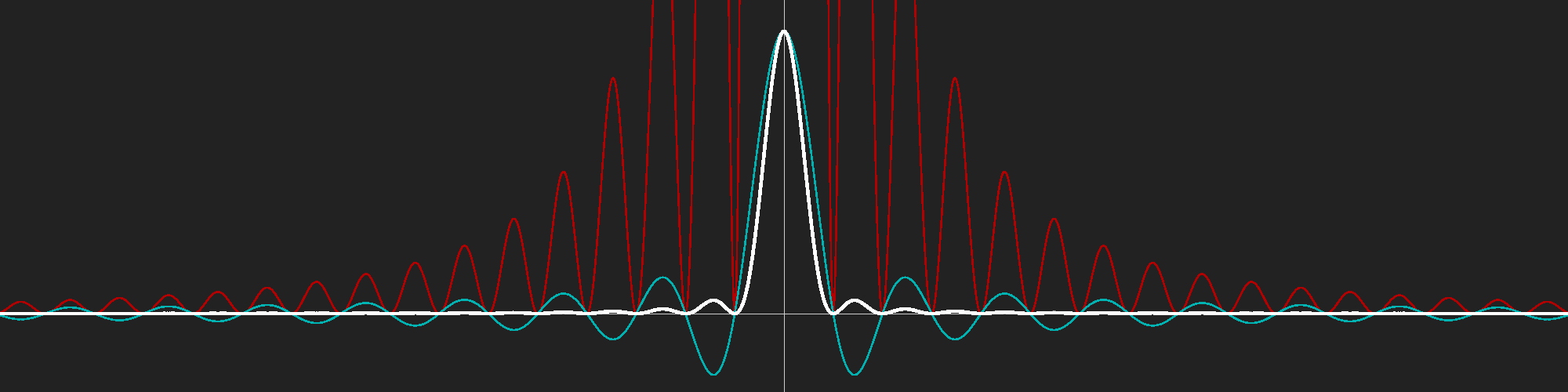
As stated above, a square aperture may be considered as two crossed slits, and thus the intensity distribution is
Assuming a digital camera with f = 10 mm and aperture f/8 (the edge of the square is then approximately 1.11 mm), the images on the sensor of a monochromatic green point light source (with λ=555 nm) and that of a white one would be given by the following pictures:
|
|
 |
 |
The width of the first and second image is 0.06 mm. The intensity is normalized to the centre.
The other two pictures are, so to say 1000 times over-exposed. The scale is different, the image width is 0.6 mm.
Click to enlarge!
For other than rectangular shapes of the aperture the intensity distribution cannot be written as a product of two functions, a two-dimensional integral over the opening is necessary. The image of a point-source has always the symmetry of the diaphragm; in addition, in the case of Fraunhofer diffraction, it is always symmetric with respect to the origin. Therefore, a pentagonal opening yields ten-pronged stars, while a hexagon produces only six-pronged ones.
or to the index page "What are the causes of colour?"