

With the naked eye, the wind turbines were hardly visible (Wide angle image, medium focal length); they were “zoomed in”. Assuming straight light rays and a straight background, this image would not be possible. But you can clearly see the mirages downwards, so the light rays that produce this mirror image are curved.
The picture was taken on March 18, 2018; the air layer directly above the water surface must have been slightly warmer than the layers above, so that the rays bend upwards. The adjacent sketch shows this schematically (and exaggeratedly). At the bottom the air is warmer, the refractive index smaller and therefore the wavelength longer than at the top.
The jagged wavy borderline between sky and water is not the horizon, but the lower edge of the mirror image. The horizon is at the height where the rotor blades and their mirror image seem to touch in the rounded bend.
A slight curvature of the light rays in the atmosphere is always present, since the density of the air and thus its refractive index depends on the altitude and the temperature. This is particularly noticeable in the case of almost horizontal lines of view. Since the density of the air generally decreases with increasing height, the rays are usually curved very weakly downwards. As a result, range of vision is larger than it would be without refraction, and this can be taken into account by using an apparent curvature slightly smaller than the curvature of the Earth's surface (larger apparent Earth radius) in the calculations. (According to Wikipedia the mean observed apparent earth radius is Rapparent ≈ 7680 km.) This will be explained in more detail below.
However, the temperature distribution plays an important role. If the temperature increases upward, the visibility can be increased strongly if the light-rays follow the earth-curvature, and there can occur even mirages upward (Fata Morgana).

According to a map of the offshore wind turbines in the German Bight, these wind turbines should belong to the wind farm Borkum-Riffgrund II.
The picture was taken at the end of June, when the weather was very warm. The water was colder than the air, so that the lower air layers were probably cooler than the slightly higher ones (inversion) and the normal trend in temperature was only reached at higher altitudes.
How much do light rays bend in the atmosphere? I do not want to present a complicated calculation here and therefore limit myself to almost horizontal beams. This condition is always fulfilled when looking at very distant terrestrial objects. As indicated in the small image above, the beam direction is always perpendicular to the wave crests.
To be concrete, we choose the zero point z = 0 of our coordinate system at eye level on the beach; the air pressure at this altitude would be 1013.25 hPa (hectopascal), which is 760 Torr (mm mercury column), and we assume 15°C as the temperature. The refractive index of the air at our zero point is n0, one meter higher is n1.
The wavelength of light in a medium is given by the wavelength in a vacuum, divided by the refractive index, i.e.
(Unit of length is the meter, that is not explicit in the equations) For a downward curvature you get a negative radius of curvature.
The refractive index of air differs only slightly from 1, the refractive index of vacuum, and this difference is proportional to the density ρ of air. Thus, for n1
Now we have all the relationships we need to calculate the radius of curvature of the approximately horizontal light beam.
You can find the required numerical values in tables or on the Internet.
As air pressure p0 we assumed 1013.25 hPa. One cubic meter at this pressure and 15°C contains 1.2250 kg of air, so the pressure difference is 1.2250 × 9.806 Pa and this results in
In order to see what influence the weather can have on the curvature of the light rays, we now also consider the case of an inversion weather situation, i.e. when the temperature does not drop with increasing altitude but rises. A typical value is a temperature rise of 1°C to 100 m height increase, i.e. 0.01 K/m.
Instead of equation (5) we use the gas equation
How can one determine the visibility range on the curved earth's surface with bent light rays? This looks quite complicated at first. But since the curvatures are very small and the sighting distances are always very small compared to the earth's radius, a simple approximation is permissible that is oriented to the optical impression: the curvature of the rays apparently reduces the curvature of the earth's surface. So you can subtract the curvature of the light rays from the curvature of the earth's surface, thereby obtaining the apparent radius of the earth and can calculate with straight rays. The adjacent sketch (in which the curvatures are very strongly exaggerated) is intended to illustrate this. The part of the windmill that disappeared behind the horizon for the eye is drawn in blue.
Curvature is defined as the change in direction (angle) per distance and is simply the inverse of the radius of curvature, as you can easily consider using the example of a circle. Thus we obtain the apparent earth radii for the two calculated cases
of 7578 km and 8912 km instead of the real value of 6371 km.
In inversion weather conditions, however, the upward temperature increase is usually not uniform and can be clearly above average in layers, so that the curvature there can also be greater than that of the earth, which can cause the rare mirages upwards.
With the help of the apparent radius of curvature Rs you can calculate the distance of the horizon or how much has already disappeared behind the horizon at a given distance as easily as without taking the refraction into account. In the adjacent sketch the invisible part of the wind turbine is drawn in blue again.
Distance of the horizon from the sea (according to Pythagoras; a: height of the eye above sea level):
the last approximation is allowed as long as a << Rs. For w you get a similar expression, and so the distance s will be
This can be used to calculate the height b of the part of the windmill that has disappeared behind the horizon.
However, it should be pointed out here that refraction cannot be easily considered in special weather situations.
It's hard to tell whether the claims that have been appearing recently on YouTube or in discussion forums that the earth is not spherical, but flat, are believed by their authors themselves, or whether there are “trolls” who make fun of putting nonsense on the net.
In the year 1865 Samuel Birley Rowbotham published under the pseudonym Parallax a script with the title “Zetetic Astronomy. Earth Not a Globe”. A second, expanded edition appeared in 1872, and a third, largely expanded edition in 1881 with illustrations by George Davey. The following quotations and illustrations are taken from the digitized original.
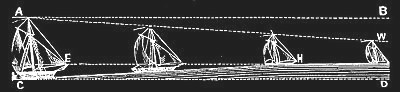
First a few lines from Rowbotham on perspective. It is a wondrous law of perspective invented by Rowbotham that has strange consequences. What is essential here is that the ground, and in particular the surface of the oceans, is not curved, but is assumed to be completely flat.

Send a young girl, with short garments, from C on towards D; on advancing a hundred yards or more (according to the depth of the limbs exposed) the bottom of the frock or longest garment will seem to touch the ground; and on arriving at H, the vanishing point of the lines C, D, and E, H, the limbs will have disappeared, and the upper part of the body would continue visible, but gradually shortening until the line A, B, came in contact with E, H, at the angle of one minute.
[…]
That part of any receding body which is nearest to the surface upon which it moves, contracts, and becomes in-visible before the parts which are further away from such surface […] The hull of a ship is nearer to the water--the surface on which it moves--than the mast head. Ergo, the hull of an outward bound ship must be the first to disappear.
And now something from one of today's Flat Earth defenders, Eric Dubay, one of his “200 Proofs Earth is Not a Spinning Ball”
139) Not only is the disappearance of ship's hulls explained by the Law of Perspective on flat surfaces, it is proven undeniably true with the aid of a good telescope. If you watch a ship sailing away into the horizon with the naked eye until its hull has completely disappeared from view under the supposed “curvature of the Earth,” then look through a telescope, you will notice the entire ship quickly zooms back into view, hull and all, proving that the disappearance was caused by the Law of Perspective, not by a wall of curved water! […]
Eric Dubay describes this alleged fact even more clearly in his children's book “The Earth Plane”, where the sun, which has already sunk halfway behind the horizon, is zoomed up again with a video camera, so that it can be seen in its entirety and when zooming further it rises higher and higher back into the sky.
This “irrefutable proof“ should be seen with one's own eyes by anyone who doubts the spherical shape of the earth. That Rowbotham's “law of perspective“ is wrong is easy to show. Straight rays of light and a straight underground presupposed, the proportions do not change as Rowbotham claims. The girl can go so far away – if the ground has no curvature, her legs never seem to disappear into the ground.

Back to the page "the origins of colour" or home.