Zweistrahlinterferenz: dünne Schichten, Doppelbrechung und Polarisation …
Dünne Schichten
Transparente dünne Schichten zeigen oft bunte Farben. Am bequemsten und deutlichsten zu beobachten ist diese Erscheinung an Seifenblasen (Bild rechts) oder Seifenlamellen.
Unten links: Seifenlamelle in einem schräg gestellten Drahtrahmen, die Licht vom
bedeckten Himmel reflektiert. Unter dem Einfluss der Schwerkraft ist
die Lamelle oben sehr dünn geworden, die Dicke nimmt nach
unten immer mehr zu.
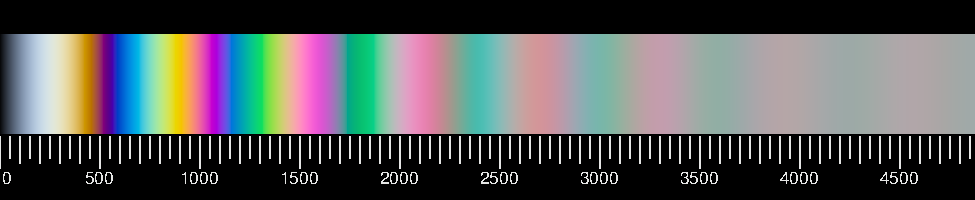
Im Bild unten rechts sehen Sie das Ergebnis einer
Rechnung.
Die unter den Farbstreifen gelegte Skala gibt die optische
Weglängendifferenz in nm (Nanometern) an.
|
 |
 | |
Die Abfolge der Farben, die man mit zunehmender Dicke sieht, ist sehr
charakteristisch, die Erscheinung ist leicht zu erklären und leicht zu
berechnen. Ein kleiner Teil der einfallenden Welle wird an der Oberseite der
Lamelle reflektiert, wobei sich das Vorzeichen des elektrischen Feldes
umdreht, ein weiterer, ungefähr gleichgroßer Teil wird an der
Rückseite der Lamelle reflektiert, und zwar ohne Vorzeichenumkehr, so
dass die Überlagerung der beiden reflektierten Wellen durch die
Differenz der beiden Wellenzüge gegeben ist.
| |
Die zu überlagernden
Wellen legen aber verschiedene Wege zurück, wie man sich an einer
Skizze leicht überlegen kann; maßgeblich ist die Differenz der
"optischen Weglänge": die zurückgelegten Wege sind jeweils mit dem
Brechungsindex des Mediums zu multiplizieren.
Wenn die Schicht sehr dünn ist, die Wegdifferenz viel kleiner als die kürzesten sichtbaren Wellenlängen, also annähernd Null ist, dann ist die Überlagerung (Differenz!) der beiden reflektierten Wellen für alle Wellenlängen sehr klein, es wird fast nichts reflektiert. Mit zunehmender Wegdifferenz steigt die reflektierte Intensität zunächst für alle sichtbaren Wellenlängen an, nimmt nach Durchlaufen des Maximums für die kürzesten Wellen zuerst wieder ab – die Lamelle erscheint gelblich, dann rötlich und dann, wenn sich die mittleren Wellenlängen auslöschen, für die das Auge am empfindlichsten ist, sehr dunkel. ...
Die relative Intensität des reflektierten Lichtes ist für alle sichtbaren Wellenlängen leicht zu berechnen; mit Hilfe der CIE-Spektralwertfunktionen xλ, yλ und zλ erhält man dann für eine vorgegebene Lichtquelle die Farbkoordinaten des reflektierten Lichts und daraus schließlich die Farbwerte für die Darstellung auf dem Bildschirm. Die Rechnung wird hier als Beispiel für alle Berechnungen von Farbkoordinaten bzw. Bildschirmfarben Schritt für Schritt erläutert und an einem Programmbeispiel (in FORTRAN) vorgeführt.
Der Anfang des berechneten Farbstreifens stimmt gut mit dem Foto überein, gegen Ende des oberen
Streifens machen sich aber schon kleine Unterschiede bemerkbar.
Welches der beiden Bilder stimmt
besser mit der Wirklichkeit überein?
Hier kommt man nicht um ein Experiment herum.
Die Aufnahme oben wurde mit einer Digitalkamera gemacht; Fotos auf Film zeigen noch größere Unterschiede.
Ich komme darauf noch zurück.
Bei der Berechnung müssen wir zwei "Strahlen" verfolgen: man spricht
deshalb von Zweistrahlinterferenz.
 | | Die Aufnahme oben wurde vor einem dunklen Hintergrund gemacht, dann kommt das ganze Licht von der Reflexion an der Lamelle. Im durchscheinenden Licht äußert sich die Zweistrahlinterferenz sehr viel schwächer, trotzdem macht sie sich bei verglasten Dias gelegentlich in Form von "Newtonschen Ringen" störend bemerkbar.
Die an der Seifenlamelle reflektierten Farben fehlen im transmittierten Licht: es erscheinen die Komplementärfarben; diese sind, da die Reflexion insgesamt nicht sehr stark ist, allerdings nur zart. |
Bei Öl auf nasser Straße ist die Überlegung dieselbe wie bei
der Seifenlamelle. Öl hat einen größeren Brechungsindex als
das Wasser darunter, daher erfolgt bei der Reflexion an der Unterseite des
Films keine Vorzeichenumkehr. Die Amplitudenunterschiede zwischen
den beiden Teilstrahlen machen sich kaum bemerkbar. Ähnlich sehen Bakterienfilme auf Wasser aus, und die Erklärung ist genau die selbe.
 |

|
|
Ölflecken breiten sich auf regennasser Straße als dünner, schillernder Film aus. | Ein Film von Bakterien auf einer schlammigen Stelle am Rand eines Teiches |
| |
 |  |
| Dünne Risse – Luftschichten – im Eis, die mit einem Hammer erzeugt wurden. (Etwa zweifach vergrößert.) | Boden eines Kochtopfes aus Edelstahl. Nach dem Kochen von Fleisch, Gemüse u.a. bildet sich manchmal eine dünne Schicht, vermutlich aus Eiweißmolekülen, die das Abwaschen übersteht und Interferenzfarben zeigt. |
Die Farben sind unabhängig davon, ob die reflektierende dünne Schicht einen größeren oder einen kleineren Brechungsindex hat als das umgebende Medium.
Die Berechnung der Farben ist bei Schichten auf Metall etwas komplizierter, aber die Farben sind sehr ähnlich. Ein Beispiel für die Berechnung wird hier gegeben.
Edelstahl ist rostbeständig, weil sich auf seiner Oberfläche eine Schicht aus Chrom(III)oxid bildet, die das Eisen vor Oxidation schützt (Passivschicht), die aber so dünn ist, dass sie nicht zu sehen ist. Ich vermute, dass die bunten Farben nicht davon herrühren, dass diese Schicht an Dicke gewinnt, sondern dass sich eine weitere transparente Schicht anlagert.
Farben dünner Schichten sind recht häufig zu beobachten. Weniger bekannt ist, dass die gleichen Farben auch auf eine andere Weise entstehen können, nämlich infolge von
Polarisation und Doppelbrechung
Anisotrope Medien, also Stoffe, deren physikalische Eigenschaften nicht in allen Richtungen gleich sind, sind doppelbrechend, wenn sie durchsichtig sind. Wir betrachten den einfacheren Fall, dass nur eine Richtung ausgezeichnet ist (Symmetrieachse, optische Achse). Tritt ein Strahl von unpolarisiertem Licht in so einen Stoff ein, so wird er in zwei linear polarisierte Teile aufgespalten, die man den ordentlichen und den außerordentlichen Strahl nennt. Beim außerordentlichen Strahl schwingt das elektrische Feld in der durch die Symmetrieachse und die Richtung des Lichtstrahls aufgespannten Ebene, beim ordentlichen senkrecht dazu.
Diese beiden Strahlen breiten sich mit verschiedener Geschwindigkeit aus, zu den beiden Strahlen gehören also verschiedene Brechungsindizes.
Davon bemerkt man im allgemeinen kaum etwas, da das Auge für die Polarisation des Lichtes nicht empfindlich ist.
Fügt man aber vor und hinter einer doppelbrechenden Probe Polarisationsfilter in den Strahlengang ein, dann ändert sich das. Das erste Polarisationsfilter sorgt dafür, dass der ordentliche und der außerordentliche Strahl beim Eintritt in die Probe in Phase sind. Wegen der verschiedenen Brechungsindizes ist die optische Weglänge der beiden Strahlen verschieden, es ergibt sich ein Phasenunterschied. Das zweite Polarisationsfilter lässt von beiden Strahlen nur je einen Teil passieren. Je nach dem Gangunterschied können sich diese beiden Anteile nun verstärken, schwächen oder auch ganz auslöschen. Auslöschung ergibt sich bei gekreuzten Polarisatoren, wenn der Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge ist. Als Folge dieser Abhängigkeit von Auslöschung und Verstärkung von den Wellenlängen ergeben sich Farben.
Bei der Untersuchung von Gesteins-Dünnschliffen zwischen gekreuzten
Polarisatoren tritt also wieder Zweistrahl-Interferenz auf: die Farben sind
dieselben wie die der Seifenblase; man kann aus den Farben auf die optische
Weglängendifferenz der beiden interferierenden Strahlen (ordentlicher
und außerordentlicher Strahl im doppelbrechenden Medium)
schließen und daraus Rückschlüsse auf die Mineralbestandteile ziehen. Zur Illustration zwei Proben unter dem
Polarisationsmikroskop.
 | |

|
Basalt mit Olivin und Pyroxen.
Bildbreite 3,3 mm.
| | Olivin,
Bildbreite 3 mm.
|
Die beiden Aufnahmen wurden
mir freundlicherweise von Prof.
Dr. W. Johannes (Universität Hannover) zur Verfügung gestellt.
Man erwartet, dass doppelbrechende Substanzen wie Kristalle oder unter Spannung stehendes Acrylglas, gedehnte Kunststoffolie u.a. zwischen Polarisationsfiltern farbig erscheinen. Aber solche Farben treten auch ohne besondere Vorrichtungen auf und wirken dann umso überraschender.


Links: Ein Acrylglaskästchen, beleuchtet mit normalem Tageslicht auf einer nicht glänzenden Unterlage – es sind keine Farberscheinungen zu beobachten.
Rechts: Im Licht vom blauen Himmel zeigt dasselbe Kästchen zarte Farben, sein Spiegelbild in der gläsernen Tischplatte erscheint sogar richtig bunt.
Das Streulicht vom blauen Himmel ist zum Teil polarisiert – das ersetzt das erste Polarisationsfilter, das an einer Glas- oder Kunstharzoberfläche schräg reflektierte Licht ebenfalls – das ersetzt das zweite Polarisationsfilter. Das im Spritzgussverfahren hergestellte Kästchen weist innere Spannungen auf, dies hat Doppelbrechung zur Folge.
Als weiteres Beispiel ein Geometrie-Dreieck aus Acrylglas, das den blauen Himmel reflektiert: Aufnahme ohne Polarisationsfilter. Bei der Aufnahme mit Polarisationsfilter wird der Reflex von der Oberseite unterdrückt und die Farben erscheinen noch kräftiger.
Fotografen verwenden Polarisationsfilter, um störende Reflexe auszuschalten oder zu mindern oder um das Himmelsblau zu vertiefen. Dabei kann es gelegentlich zu Farberscheinungen kommen, wie das folgende Beispiel zeigt:

Doppelbrechung von Eis: Bruchstücke des dünnen Eises auf einem zugefrorenen Teich wurden so an anderer Stelle auf das Eis gelegt, dass darunter luftgefüllte Zwischenräume blieben, und mit einem Polarisationsfilter fotografiert.
Ohne das Polarisationsfilter würde sich der helle (graue) Himmel in den Platten spiegeln, aber das an der Oberseite reflektierte Licht wird durch das Filter unterdrückt. Das an der Unterseite der Eisplatten und dem darunter liegenden Eis reflektierte Licht ist ebenfalls linear polarisiert, das Eis darüber ist doppelbrechend, und so ergibt sich wieder die Situation eines doppelbrechenden Mediums zwischen zwei Polarisatoren. Die großen einzelnen Kristalle im Eis sind verschieden orientiert, daher zeigen manche Bereiche keine Farben und andere sind nur ganz schwach farbig.
Noch drei ähnliche Bilder: (1), (2), (3). Nr. 1 bei bedecktem Himmel wie oben, Nr. 2 und 3: eine Eisplatte wird vor die Spiegelung der Sonne in der Eisfläche des Teiches gehalten und durch ein Polarisationsfilter betrachtet bzw. fotografiert.
|
Da an dünnen Rissen im Eis die gleichen Farben auftreten können (Bild rechts), werden die durch Doppelbrechung entstehenden leicht als Farben dünner Schichten fehlinterpretiert. (Für das Foto rechts wurde kein Polarisationsfilter verwendet!) |  |
| Ein weiteres Beispiel für Farbentstehung infolge Doppelbrechung: Kaleidoskop Calcit |  |
Quételetsche Ringe oder Streifen
Eine selten zu beobachtende Farberscheinung. Ohne die Fotos von Eva Seidenfaden hätte ich nicht danach gesucht.

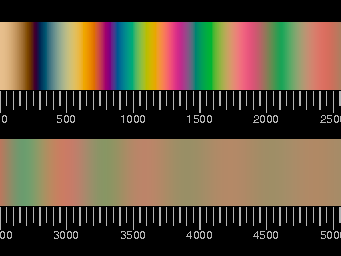
Links: Quételetsche Streifen auf einem mit Stärkepulver angestaubten und mit einem Halogenstrahler beleuchteten Spiegel.
Rechts: Berechnete Farbenfolge für diesen Fall von Zweistrahlinterferenz; als Farbtemperatur der Lichtquelle wurde 3500 K angenommen. Die Skala gibt wieder den optischen Wegunterschied in Nanometern an.
Die beiden interferierenden Strahlen sind in diesem Fall: das Licht, das an einem Staubkorn auf der Glasoberfläche gestreut wird, dann in das Glas eindringt, an der (verspiegelten) Rückseite reflektiert wird und schließlich zum Beobachter gelangt, und das Licht, das zuerst ins Glas eindringt, an der Rückseite reflektiert und dann erst von dem Staubkorn zum Beobachter gestreut wird.
Auf einer Linie, die scheinbar durch das Spiegelbild der Lichtquelle verläuft, ist der Wegunterschied der beiden Strahlen Null, dort verstärken sich die beiden Strahlen maximal. Wenn die Lichtquelle und das Auge des Beobachters gleich weit vom Spiegel entfernt sind, dann ist diese Linie eine Gerade. Ist der Abstand der Lichtquelle kleiner, dann ist diese Linie ein Kreisbogen und zum Spiegelbild des Beobachters konvex, ist die Lichtquelle weiter weg als der Beobachter, so ist sie zum Spiegelbild des Beobachters konkav. Eine einfache Rechnung zeigt, dass die Streifen (bei einem planparallelen Spiegel) konzentrische Kreise sind.
Hier gibt es eine ausführlichere Beschreibung des Effekts. Den Versuchsaufbau finden Sie im Internet: [1], [2] mit Beispielen von Beobachtungen unter freiem Himmel.
Weiter zur Vielstrahl-Interferenz,
zurück zur Beugung
oder zurück zur Übersicht: Wie kommt Farbe zustande?






