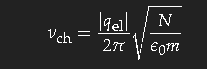Dietrich Zawischa

Kristalle, Mineralien,
Metalle, Pigmente

Azurit, ein basisches Kupferkarbonat, wurde seit dem Altertum zur Herstellung blauer Farbe verwendet und wurde erst in neuerer Zeit durch künstlich hergestellte Pigmente verdrängt.

Natrium, in Spuren in eine Flamme gebracht, färbt diese auffallend gelb. Licht genau dieser Wellenlängen, die es emittieren kann, kann Natrium in atomarer Form (Natriumdampf) auch absorbieren. Dies führt allerdings nicht dazu, dass der Dampf farbig erscheint, die Absorption kann man nur mit Hilfe eines Spektroskops überhaupt wahrnehmen. Natrium kommt in der Natur nicht als elementares Metall vor. Das schwach gebundene Valenzelektron, das „Leuchtelektron“, wird nämlich leicht abgegeben. In einer Kochsalzlösung ist das Natrium ionisiert, die Elektronen in den Na⁺-Ionen „sitzen“ in sehr stabilen abgeschlossenen Schalen (Edelgaskonfiguration), und die Photonenenergie des sichtbaren Lichtes reicht nicht aus, elektronische Anregungen zu erzeugen. In der Kochsalzlösung befinden sich die vom Natrium abgegebenen Elektronen an den Chlorionen, Cl^–, die mit Hilfe des zusätzlichen Elektrons ebenfalls eine stabile Edelgaskonfiguration erreichen – und daher aus den gleichen Gründen ebenfalls farblos sind. Eine Kochsalzlösung ist deshalb so klar wie reines Wasser.
Auch in den Wassermolekülen selbst können elektronische Anregungen erst durch ultraviolette Strahlung bewirkt werden – reines Wasser ist klar. Erst bei dicken Schichten bemerkt man die schwach grünlichblaue Farbe, die durch die schwache Absorption unter Anregung von Molekülschwingungen zustandekommt.
Ganz allgemein kann man feststellen, dass Verbindungen der ersten drei Perioden des Periodensystems, solange die Moleküle nur aus wenigen Atomen bestehen, farblos sind.

Farbgebende Ionen

Mit zunehmender Zahl der Ladungen im Kern eines Atoms und entsprechend zunehmender Elektronenzahl wird das atomare Termschema immer komplizierter. Im folgenden interessieren wir uns besonders die Eigenschaften einer nur zum Teil gefüllten 3d-Schale, wie sie bei den Übergangselementen Chrom, Mangan, Eisen, Kobalt, Nickel und bei Kupfer(II)ionen vorliegt.

Im Kristallfeld

Unter den schwereren Elementen haben besonders die Ionen der Übergangselemente die Fähigkeit, innerhalb des sichtbaren Spektralbereiches zu absorbieren, wenn sie sich in einem Kristallgitter befinden.

Während im Idealfall eines isolierten Ions die Elektronen nur das Kraftfeld des eigenen Kerns und der übrigen Elektronen desselben Ions spüren, äußert sich im Kristall die Anwesenheit der Nachbarn durch zusätzliche Kräfte. Beim Einbau solcher Ionen in chemische Verbindungen bzw. Kristallgitter werden diese Niveaus nämlich durch Wechselwirkung mit den Nachbarn etwas verschoben, je nach räumlicher Orientierung nach oben oder nach unten, abhängig von der Art der Umgebung bzw. der Bindung. Die verschobenen Niveaus werden auch zu schmalen Bändern aufgespalten, wie weiter unten beschrieben.

Qualitativ lässt sich die Wirkung eines Kristallfeldes in unserem Wasserbecher-Modell veranschaulichen: würde der Becher z.B. durch zwei benachbarte Becher etwas zusammengequetscht, so dass der Querschnitt oval wird, so würde das Wasser in Richtung der kurzen Achse des Ovals schneller hin- und herschwappen als in Richtung der langen Achse.

			Andere Schwingungsformen werden ebenfalls betroffen, und zwar je nach ihrer räumlichen Ausbildung verschieden stark. Durch Doppelklicken auf eines der Bilder können Sie die Animation einschalten, einfaches Klicken schaltet sie wieder aus. Durch Klicken auf das Symbol ◊ unter dem jeweiligen Bild kann die Animation auch in einem separaten Fenster gestartet werden.
◊	◊

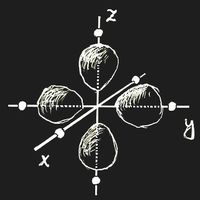
Bei den genannten Elementen bzw. ihren Ionen ist die 3d-Schale teilweise besetzt. Die Form der Elektronenwolken ändert sich gegenüber den beim Wasserstoff gezeigten nur wenig (und nur in radialer Richtung).
Denken wir uns ein Ion mit einem einzigen 3d-Elektron, Sc²⁺ oder Ti³⁺, in ein Kristallgitter eingebaut. Als Koordinatenursprung wird der Ort des betrachteten Kations gewählt. Ein sehr häufiger und wichtiger Fall ist der, dass das Ion so von sechs negativ geladenen Ionen umgeben ist, die alle den gleichen Abstand vom Ursprung haben und auf den Koordinatenachsen sitzen. Man nennt dies eine oktaedrische Konfiguration: die umgebenden Anionen sitzen an den Ecken eines regelmäßigen Oktaeders, dessen Mittelpunkt der Koordinatenursprung ist.


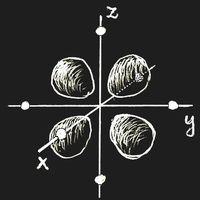(a)		(b)

Für ein einzelnes Ion ohne äußeres Feld sind alle Orientierungen der Elektronenwolke gleichwertig und die Energie ist von der Orientierung unabhängig. Das ändert sich durch das von den Nachbarn hervorgerufene elektrische Feld. Wenn die Teil-Ladungswolken des Elektrons genau in die Richtung zu benachbarten negativen Ionen zeigen (Bild a), dann ist die Energie größer als in den Fällen, wo die Elektronendichte entlang der Koordinatenachsen verschwindet (Bild b). Diese Energiedifferenz nennt man Δ. Natürlich verändern sich durch das Feld der Nachbarionen auch die Wellenfunktionen selbst, aber dies ist in gröbster Näherung vernachlässigbar.
Im Grundzustand wird das eine 3d-Elektron also einen Zustand vom Typ (b) besetzen, und es besteht die Möglichkeit, dass durch ein eingestrahltes elektromagnetischen Feld mit der richtigen Frequenz ν = Δ/h ein Übergang in eines der energetisch höherliegenden Niveaus hervorgerufen wird, also Strahlung absorbiert wird.

Betrachten wir nun ein Ion mit mehr als einem d-Elektron. Die Elektronen stoßen sich gegenseitig ab und diese Wechselwirkung führt schon im Fall des freien Ions zu einer Aufspaltung der Niveaus mit verschiedenem Gesamt-Bahndrehimpuls („Grobstruktur“), darüber hinaus besteht auch Wechselwirkung zwischen Spin- und Bahndrehimpuls, was zu einer weiteren Niveauaufspaltung je nach Gesamtdrehumpuls („Feinstruktur“) führt. Für die leichteren Elemente ist die Spin-Bahn-Wechselwirkung gering. Solange kein äußeres Feld vorhanden ist, ist im Raum keine Richtung ausgezeichnet, und daraus folgt wieder, dass Zustände, die sich nur durch die Lage im Raum unterscheiden, die gleiche Energie haben, und darüber hinaus hat dies zur Folge, dass der Drehimpuls erhalten ist und die Zustände durch die Quantenzahlen des Drehimpulses gekennzeichnet werden können.
Es zeigt sich, dass sich der Einfluss der Coulombwechselwirkung zwischen den Elektronen einer Schale in (zunächst empirisch gefundene) einfache Regeln für den Grundzustand zusammenfassen lässt.

Hundsche Regeln:
– Volle Schalen oder Unterschalen haben Gesamt-Drehimpuls und Gesamtspin null.
– Der Gesamtspin S nimmt den maximal möglichen Wert an, die Spins der einzelnen Elektronen stehen also möglichst parallel.
– Von mehreren Zuständen mit gleichem Gesamtspin hat der Zustand mit dem größten Bahndrehimpuls die niedrigste Energie
– Ist die Schale weniger als halbvoll, so ist der Gesamtdrehimpuls J = | L – S |; ist sie mehr als halbvoll, so ist J = L + S

Das dreifach positiv geladene Ion Cr³⁺ hat außerhalb der abgeschlossenen Schalen (Argon-Konfiguration) drei Elektronen in der 3d-Schale. Um den den Hundschen Regeln entsprechenden Grundzustand zu finden, konstruiert man den Zustand mit der maximalen z-Komponente des Gesamtspins und des Bahndrehimpulses. Die drei Einzelspins stehen parallel, also ist S = 3/2. Gemäß dem Pauli-Prinzip können dann die Einteilchenzustände mit m = 2, m = 1 und m = 0 von je einem Elektron besetzt werden, die Summe ist M = 3 und daher ist auch L = 3. In spektroskopischer Notation wird der erhaltene Zustand mit ⁴F bezeichnet. Der obere Index bezeichnet die Anzahl der Spin-Einstellmöglichkeiten 2S + 1, der Bahndrehimpuls wird, für Mehrteilchensysteme in Großbuchstaben, wieder durch die traditionellen Buchstaben S, P, D, F, . . . für L = 0, 1, 2, 3, . . . angegeben.
Als nächsthöheres Niveau ergibt sich nach den Hundschen Regeln das Multiplett ⁴P.

Korund, Al₂O₃, und Beryll, Be₃Al₂Si₆O₁₈ sind im reinen Zustand farblos. Ersetzen Chrom(III)-Ionen in Prozentbruchteilen Aluminium-Ionen, so wird Korund zum Rubin, Beryll zum Smaragd. In beiden ist das Chrom-Ion von sechs Sauerstoffionen in (leicht verzerrter) oktaedrischer Anordnung umgeben, aber, aufgrund der verschiedenen chemischen Zusammensetzung ist das Feld im Smaragd etwas schwächer als im Rubin. Was wird aus dem F-Multiplett im oktaedrischen Kristallfeld?

Links: Rubin, rechts: Smaragd. Sowohl im Rubin als auch im Smaragd rührt die Farbe von Chromionen her, die wenige Prozent der Aluminiumionen ersetzen. Beide Bilder (von einer
Edelstein- und Mineralienbörse) vergrößert; die Breite des Bildausschnittes beträgt je ca. 3 cm.

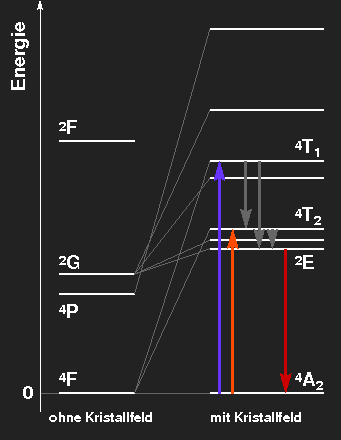
Die Symmetrieeigenschaften der Dichteverteilung von drei zu einem F-Zustand gekoppelten Elektronen sind dieselben wie die von einem f-Elektron. Unter den f-Wellenfunktionen (l = 3) ist eine, die bei allen Symmetrieoperationen, die das Oktaeder in sich selbst überführen, ebenfalls in sich selbst übergeht (von unerheblichen Vorzeichenwechseln abgesehen). Sie lässt sich als xyzf(r) schreiben, und die zugehörige Dichteverteilung besteht aus acht Wölkchen, deren Zentren die Ecken eines Würfels bilden. Dadurch weichen sie den negativen Ionen in oktaedrischer Anordnung optimal aus und haben demzufolge die niedrigste Energie. Dass sich aber die restlichen sechs f-Wellenfunktionen zu zwei Tripletts kombinieren, ist nicht mehr so leicht zu sehen.


Rubin		Smaragd

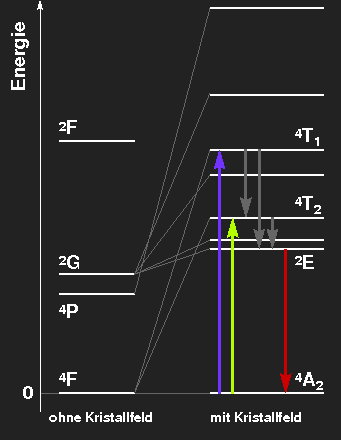
Termschema des Cr³⁺-Ions, das die Aufspaltung der Niveaus durch das oktaedrische Kristallfeld zeigt. Die Niveauabstände entsprechen im linken Bild ungefähr denen im Rubin, im rechten denen des Smaragds.

Rubin: Die rote Farbe kommt daher, dass violettes und gelbgrünes Licht absorbiert werden kann, dieses fehlt dann im durchgelassenen Licht, das hauptsächlich Rot und ein wenig Blau enthält. Die angeregten Niveaus geben ihre Energie durch Wärmestrahlung oder thermische Wechselwirkung (mit Gitterschwingungen) wieder ab, wodurch das mit ²E bezeichnete Niveau bevölkert wird. Die Übergänge von dort in den Grundzustand haben rote Fluoreszenz zur Folge, zur Farbe des Steins tragen sie nicht bei, aber man sieht die Farbe bei Bestrahlung mit ultraviolettem Licht oder im Licht des Rubinlasers. Die Anregung der aus dem ²G hervorgehenden Zustände aus dem Grundzustand erfolgt nur mit verschwindender Wahrscheinlichkeit, weil ein Umklappen des Spins erforderlich wäre.

Fluoreszenz des Rubins: Links: Rubin im Muttergestein (Fundort: Froland, Norwegen), im Tageslicht Rechts: dasselbe Stück bei Beleuchtung mit langwelligem UV („Schwarzlicht“).

Smaragd: Das etwas schwächere Kristallfeld hat eine etwas schwächere Niveauaufspaltung zur Folge. Die Absorptionsmaxima liegen im orangeroten und blauvioletten Bereich, grünes Licht wird durchgelassen. Die rote Fluoreszenzlinie ist gegenüber dem Rubin kaum verändert.
Die Aufspaltung der Niveaus zu Energiebändern, die weiter unten behandelt wird, ist hier noch nicht berücksichtigt.
Eisen- und Titanbeimengungen machen den Saphir (ebenfalls Korund) blau. Chrysopras ist durch geringe Beimengung von Nickel grün gefärbter Chalzedon (ein mikrokristalliner Quarz), während die rötliche und bräunliche Farbe der Kieselsteine (aus Quarz) durch Eisenionen hervorgerufen wird.

Amethyst ist ein durch Eisenionen Fe⁴⁺, die von vier Sauerstoffionen umgeben sind, violett gefärbter Quarz (laut Wikipedia; die genaue Struktur der Farbzentren scheint noch nicht völlig geklärt zu sein). Das Bild zeigt einen Ausschnitt aus einer Amethystdruse aus Brasilien, ca. natürliche Größe.

Die durch Fremdatome in geringer Konzentration hervorgebrachten Farben von Mineralien, die ansonsten farblos wären, kommen nur durch die Durchsichtigkeit der Kristalle zur Geltung. Die Kristalle sind sozusagen nur schwach gefärbt; in pulverisiertem Zustand ist von der Farbe nichts mehr zu bemerken. Die Farbe des Pulvers ist als „Strichfarbe“ ein Hilfsmittel zur Bestimmung von Mineralien; ein Strich mit dem fraglichen Mineral auf einem Porzellantäfelchen offenbart sie, und für die eben besprochenen Fälle ist sie weiß.

Pleochroismus

Pleochroismus, „Mehrfarbigkeit“ (Dichroismus, Trichroismus) kann man bei manchen Kristallen beobachten, die nicht im kubischen System kristallisieren. Bekanntestes Beispiel dafür dürfte der Turmalin sein.

Die drei Bilder zeigen ein kleines Turmalin-Kristallbruchstück (L=28 mm), aufgenommen ohne Filter (oben) und mit einem Polarisationsfilter, Durchlassrichtung (elektrisches Feld) parallel zur Kristallachse (Mitte) und Durchlassrichtung senkrecht auf die Kristallachse (unten).

Turmalinkristalle zeigen oft an einem Stück verschiedene Farben, so wie auch das gezeigte Exemplar, das im linken Drittel himmelblau und sonst grün ist, aber das ist hier nicht gemeint, sondern der Sachverhalt, dass sich die Farbe für verschiedene Polarisationsrichtungen des Lichts unterscheidet, was die unteren beiden Bilder zeigen.

Wie oben am Beispiel des Rubins und Smaragds besprochen, führt die Einbettung in das Kristallfeld zu einer Aufspaltung der Energieniveaus des farbgebenden Ions. Je geringer die Symmetrie des Kristallfeldes, desto komplizierter wird diese Aufspaltung. So ergibt sich beispielsweise im grünen Turmalin, dass Licht mittlerer Wellenlängen (grünes Licht) nicht absorbiert wird, wenn das elektrische Feld in Richtung der Kristallachse schwingt („außerordentlicher Strahl“), dahingegen stark absorbiert wird, wenn die Schwingungsrichtung senkrecht zur Achse ist („ordentlicher Strahl“).

Turmalin (trigonal, mit dreizähliger Symmetrieschse) ist als optisch einachsiger Kristall dichroisch; mehr als eine optisch ausgezeichnete Richtung kann Trichroismus zur Folge haben.

Früher wurden Turmalinplättchen zur Untersuchung der Polarisation des Lichts verwendet; heute dienen künstlich (nach dem von Edwin H. Land erfundenem Verfahren) hergestellte dichroische Folien als Polarisationsfilter.

Im Komplex

Der kompliziertere Aufbau der schwereren Elemente, insbesondere der Übergangselemente, äußert sich aber auch in schwieriger zu erfassenden Formen von chemischer Bindung.

Die Absenkung eines Energieniveaus durch die Wechselwirkung mit Nachbaratomen, -Molekülen oder Ionen bedeutet, dass für das Gesamtsystem ein energetisch günstigerer Zustand möglich ist, also eine Art von Bindung. Da die Teilsysteme der Quantenmechanik unterliegen, arrangieren sich in diesen Fällen die Wellenfunktionen so, dass die Energie im Grundzustand minimal wird. Näherungsweise lassen sich die Wellenfunktionen (Orbitale) des Gesamtmoleküls als Überlagerungen (Linearkombinationen) der Orbitale der beteiligten Atome bzw. Ionen auffassen; man unterscheidet bindende und antibindende Orbitale (die zu Anziehung bzw. Abstoßung beitragen) genau wie sonst auch im Fall der kovalenten Bindung.
Man spricht in Fällen, wo sich „Nebenvalenzen“, Elektronen in Niveaus unterhalb der Valenzniveaus, an der Bindung beteiligen, von Komplexbildung. Die angelagerten Moleküle oder Ionen werden Liganden genannt. Häufige Liganden sind die Halogenid-Ionen, OH^–, H₂O, NH₃, NO₂^–, CN^–.
Wesentlich für die Farbigkeit von Metallkomplexen ist einerseits die Aufspaltung der im sphärisch-symmetrischen Fall alle zur gleichen Energie gehörigen Niveaus der nur teilweise besetzten Schalen durch das von den Liganden hervorgerufene elektrische Feld, wodurch Übergänge innerhalb dieser Schalen überhaupt erst möglich werden, andererseits die Ausweitung der Atomorbitale zu wesentlich größeren Molekülorbitalen, wodurch größere Absorptionswahrscheinlichkeiten für sichtbares Licht möglich werden. (Der Zusammenhang zwischen Molekülgröße und Übergangswahrscheinlichkeit wurde in dem Aufsatz über Farbstoffe besprochen.) Verzerrung der Wellenfunktionen und geringe Beimischungen von Anteilen anderer Symmetrie kann Übergänge ermöglichen, die sonst durch die Symmetrie verboten wären („Auswahlregeln“).

Im Kupfersulfat CuSO₄·5H₂O sind die fünf Wassermoleküle unterschiedlich gebunden. Vier davon sind quadratisch-planar an Cu²⁺ koordiniert und lassen sich durch Erhitzen bis 100ºC abspalten. Das fünfte Wassermolekül sitzt über H-Brücken am Sulfat-Anion und lässt sich erst oberhalb von 200ºC abspalten. Beim Erhitzen verliert das Salz mit dem Wasser auch seine blaue Farbe und wird weiß.

Kupfersulfat (Kristallbruchstücke)

Hier konnten nur die Grundgedanken aufgezeigt werden; für ausführlichere und tiefergehende Erklärungen der chemischen Bindung und der Komplexverbindungen im Rahmen der Ligandenfeldtheorie muss auf die einschlägigen Lehrbücher der Chemie und der Festkörperphysik verwiesen werden.

Erwähnt sei noch ein Mechanismus, der in Komplexverbindungen auch vielfach zum Tragen kommt:

Ladungsübertragung für kräftige Farbe

Mit dem Ausdruck „Ladungsübertragung“ (englisch: charge transfer) bezeichnet man einen Mechanismus, der dem im Abschnitt Farbstoffe am Beispiel des Fuchsins behandelten entspricht.
Verbindungen, die das gleiche Element in verschiedenen Oxidationsstufen enthalten, sind häufig farbig, d.h. sie können Licht stark absorbieren. Als Beispiel sei hier der Magnetit genannt, FeO·Fe₂O₃. Der chemischen Formel nach besteht eine Einheit Fe₃O₄ aus einem Fe²⁺-Ion, zwei Fe³⁺-Ionen und vier O^2–-Ionen. Aber die Quantenmechanik erlaubt Zustände, in denen sich ein Elektron über drei Fe³⁺-Ionen verteilt, so dass man nicht sagen kann, welches davon nun das zweiwertige Ion ist. So ähnlich wie bei einer schwingenden Saite gibt es dann eine Grundschwingung niedrigster Energie und Oberschwingungen, bei denen Teile des Welle in Gegenphase zueinander schwingen. Überlagert man Grund- und ersten Anregungszustand, so beobachtet man eine heftige Oszillation der Ladungsverteilung über eine verhältnismäßig große Distanz. Daran kann man sehen, dass unter Einfluss einer elektromagnetischen Welle sehr leicht Übergänge zwischen den beiden Zuständen erfolgen können, ein Molekül dieser Art absorbiert Licht der passenden Frequenz sehr stark. Diese Eigenschaft bleibt erhalten, wenn sich viele Einheiten zu einem Kristall zusammenschließen; durch die gleich zu besprechende Aufspaltung von Energieniveaus in Energiebänder wird der Bereich der absorbierbaren Frequenzen noch gewaltig erweitert.

Magnetitkristall im Muttergestein. Magnetit kann Licht aller Frequenzen absorbieren und ist daher schwarz, auch sein Strich ist schwarz, er ist stark farbig (wenn auch nicht bunt). Künstlich hergestelltes Magnetit-Pigment ist als Eisenoxidschwarz im Handel.

Ladungsübertragung kommt nicht nur zwischen gleichartigen Ionen vor: im Saphir geschieht sie zwischen Eisen- und Titan-Fremdatomen im Kristallgitter des Korund. Eisen und Titan können als Fe²⁺ und Ti⁴⁺ oder, mit höherer Energie, als Fe³⁺ und Ti³⁺ ins Kristallgitter eingebaut sein. Der energetisch niedrigste Zustand eines Eisen-Titan-Paares ist eine Überlagerung aus beiden Möglichkeiten, so dass das Eisen etwas mehr als zweifach, das Titan etwas weniger als vierfach positiv geladen ist, wobei sich ein Elektron partiell beim Eisen und beim Titan aufhält, mit gleichem Vorzeichen der Wellenfunktion in beiden Ionen („bindender Zustand“). Ein ähnlicher („antibindender“) Zustand, bei dem das Vorzeichen der Wellenfunktion an den beiden Ionen verschieden ist, liegt energetisch etwas höher und kann unter Absorption von Licht angeregt werden.
Man kann auch Übergänge zwischen bindenden und antibindenden Molekülorbitalen als Ladungsübertragung beschreiben, dies kann in Komplexverbindungen zu kräftiger Farbe führen, wenn die Übergangsfrequenzen im sichtbaren Bereich liegen. Auf die Termschemata von Komplexverbindungen kann aber hier nicht eingegangen werden.


Malachit, Cu₂CO₃(OH)₂	Azurit, Cu₃(CO₃)₂(OH)₂

Schon im Altertum wurden Malachit und Azurit zur Pigmentherstellung verwendet; heute werden diese Pigmente nur noch zur Restauration alter Bilder eingesetzt.

Festkörper

Das, was geschieht, wenn sich Atome zu Molekülen oder zu Festkörpern zusammenschließen, ist durch den Sachverhalt, dass Teilchen Welleneigenschaften haben, bestimmt. Nun sind aber die Eigenschaften von Wellen und Schwingungen weitestgehend unabhängig von der schwingenden Substanz. Diese Eigenschaften, die die mikroskopische Physik bestimmen, kann man daher auch schon an makroskopischen Wellen oder schwingenden Systemen sehen.
Jedem für ein Elektron in einem einfachen Atom möglichen Zustand entspricht, wie wir gesehen haben, eine Schwingungsform der Wellenfunktion, zu der eine bestimmte Frequenz gehört. Wir wählen als Analogon für einen Zustand eines Atoms ein Pendel; ein anderes Atom im gleichen Zustand wird durch ein zweites, gleiches Pendel repräsentiert. Die Frequenzen der beiden Pendel sind gleich. Bringen wir die Atome einander nahe, so wird durch die elektrischen Kräfte eine Wechselwirkung zwischen beiden auftreten. 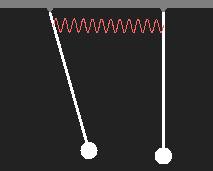Dieser entspricht bei den Pendeln eine Kopplung, die wir durch eine schwache Feder künstlich anbringen können. Was passiert?

		Animierte Grafiken auf dieser Seite können durch Doppelklicken auf das Bild eingeschaltet und durch einfaches Klicken wieder ausgeschaltet werden. Durch Klicken auf das Symbol ◊ unter dem jeweiligen Bild kann die Animation auch in einem separaten Fenster gestartet werden. Hier sehen Sie die Bewegung von zwei gekoppelten Pendeln nach dem anfänglichen Auslenken nur eines Pendels.
◊

Uns interessieren besonders die Zustände mit harmonischer Zeitabhängigkeit (d.h. alle Teile des Systems führen sinusartige Schwingungen mit der gleichen Frequenz aus), weil diese wegen E = hν den quantenmechanischen Zuständen fester Energie entsprechen. Ohne Kopplung haben beide Pendel die gleiche Frequenz; mit Kopplung gibt es nur zwei einfach periodische Schwingungsformen mit unterschiedlicher Frequenz: Im einen Fall bewegen sich die Pendel gleichsinnig mit der ursprünglichen Frequenz (die Länge der koppelnden Feder bleibt konstant), im anderen Fall gegensinnig, wobei aber die rücktreibende Kraft durch die Feder vergrößert wird, daher mit etwas erhöhter Frequenz.


◊	◊

Tragen wir die Frequenzen in ein Diagramm ein, so erhalten wir für zwei Pendel das unten links gezeigte „Termschema“.

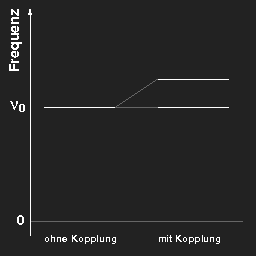
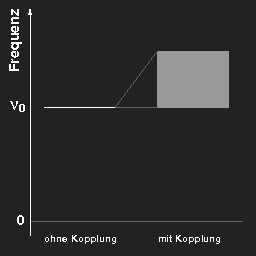Links: Die Freqauenzen von zwei gleichen Pendeln ohne und mit Kopplung. Rechts: dasselbe für eine Reihe von „unendlich“ vielen Pendeln.

Dass bei gekoppelten Pendeln die niedrigste Frequenz gleich der von ungekoppelten Pendeln ist, ist ein Spezialfall; im allgemeinen ergibt sich diese Übereinstimmung nicht.
Bei drei gekoppelten Pendeln findet man drei verschiedene Eigenschwingungen und Eigenfrequenzen, für eine Reihe von N gekoppelten Pendeln eine Aufspaltung in N verschiedene Frequenzen, und wenn N sehr groß wird, „gegen unendlich geht“, dann ergibt sich für die gekoppelten Pendel im Grenzfall ein kontinuierliches Band von möglichen Frequenzen von ν_min bis ν_max, wie in dem Bild oben rechts gezeigt.

Qualitativ ist all dies auf Atome übertragbar, wobei wir bedenken, dass immer die Energie proportional zur Frequenz ist, und es gilt für jedes Energieniveau.
Denken wir uns einzelne Atome einer Substanz aneinandergefügt, bis schließlich das Raumgitter eines Kristalls aufgebaut ist, und betrachten wir die möglichen Energien der lockersten gebundenen Elektronen. Für das isolierte Atom haben wir ein Niveauschema mit scharf definierten Energien, von denen die niedrigsten im Grundzustand besetzt gedacht sind. Für jedes Energieniveau gilt entsprechend, was wir bei den gekoppelten Pendeln gesehen haben, eine Aufspaltung der möglichen Energien in immer mehr benachbarte Niveaus, die sich im Fall von quasi unendlich vielen Atomen zu Energiebändern vereinen. So eine Bänderstruktur ergibt sich auch, wenn zwei oder mehrere Arten von Atomen zu einem Kristall vereinigt werden. Da die Wechselwirkung der Elektronen mit den Nachbaratomen umso schwächer ist, je näher sie sich am Kern des eigenen Atoms aufhalten, je stärker gebunden sie also sind, ist die Aufspaltung der höheren Niveaus größer als die der tiefliegenden; für die zum „Ionenrumpf“ gehörigen Elektronen ändert sich wenig.
Nach wie vor gilt das Pauli-Prinzip, dem zufolge gleiche Teilchen (Elektronen) sich nicht in gleichen Zuständen befinden können.

Betrachten wir als erstes einen Steinsalzkristall. Steinsalz, chemisch Natriumchlorid. Das Natriumion hat dieselbe Elektronenkonfiguration wie das Edelgas Neon, das Chlorion wie das Edelgas Argon. Edelgaskonfigurationen sind sehr stabil, d.h. um sie anzuregen braucht man viel mehr Energie als die Photonen des sichtbaren Lichts mitbringen. Die Energieniveaus der Natrium- und der Chlorionen werden durch die Wechselwirkung im Kristall zwar zu Bändern aufgespalten, aber die große Energielücke zwischen den von Elektronen besetzten und den niedrigsten unbesetzten Zuständen bleibt bestehen. Licht kann daher nicht absorbiert werden, ein reiner Kochsalzkristall ist farblos und durchsichtig.

Steinsalz-Kristallstufe aus Wieliczka, Polen im Naturhistorischen Museum, Wien.

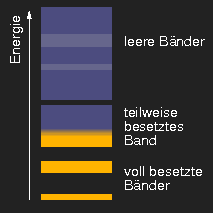
Ganz anders Kristalle aus Atomen, bei denen die äußerste Schale erst zum kleinen Teil besetzt ist: in einem aus solchen Bausteinen bestehenden Kristall liegen unbesetzte Energieniveaus dicht neben besetzten, es ist nur ein geringer Energieaufwand nötig, um die Verteilung der Elektronen zu ändern. Dadurch werden die Elektronen innerhalb des Kristalls fast frei beweglich – die Substanz ist metallisch. Die optischen Eigenschaften von Metallen werden weiter unten behandelt.
Metalle zeichnen sich durch ihre elektrische Leitfähigkeit aus. Stromtransport kann in einem Festkörper nur erfolgen, wenn nicht alle Energiezustände in einem Band von Elektronen besetzt sind. Dafür eine Plausibilitätserklärung: Stellen wir uns vor, die vielen Zustände in einem Band seien eingeteilt in solche, bei denen sich das Teilchen nach links bewegt, solche, bei denen es sich nach rechts bewegt, und solche, bei denen es weder nach links noch nach rechts läuft. Es müssen genausoviele Zustände für Ladungstranspart nach links vorhanden sein wie für Ladungstransport nach rechts, und wenn alle besetzt sind, so gleicht sich der F1uss nach links mit dem nach rechts exakt aus. Und auch, wenn Spannung angelegt wird, ändert sich daran nichts, da ja nach wie vor alle nach links und alle nach rechts transportierenden Zustände besetzt sind: wieder summieren sich beide Flüsse exakt zu Null. Wenn aber ein Band nur teilweise gefüllt ist, dann kann bei angelegter Spannung eine Umverteilung erfolgen, so dass mehr Ladung in die eine als in die andere Richtung fließt, also ein elektrischer Stromtransport erfolgt.


Isolator	Metall	Halbleiter

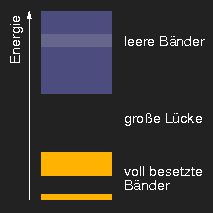
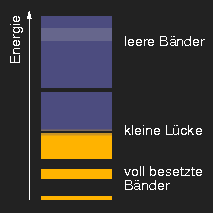
Schematische Darstellung typischer Bandstrukturen. (Die helleren Bereiche in den unbesetzten Bändern sollen andeuten, dass sich die aus verschiedenen Niveaus hervorgehenden Bänder überlappen können.)

Je nach der Größe der Energielücke zwischen den besetzten und leeren Bändern bzw. der Existenz von teilweise besetzten Bändern ergibt sich die Einteilung der Stoffe nach ihren elektrischen Eigenschaften in Isolatoren, Metalle und Halbleiter.

Bandstruktur und Farbigkeit

Die Bandstruktur bestimmt auch die optischen Eigenschaften. Nichtleiter, wie Diamant, Kochsalz, Eis, Zucker, Kalkspat und viele andere weisen eine große Lücke zwischen dem letzten vollbesetzten und dem ersten leeren Band auf. Diese Lücke ist so groß, dass ein Energiequant aus dem Bereich des sichtbaren Lichts nicht ausreicht, ein Elektron aus dem besetzten ins leere Band zu heben – daher kann das Quant auch nicht absorbiert werden, und die Kristalle sind in reinem Zustand glasklar.
Bei anderen kristallinen Substanzen ist die Lücke zwischen dem letzten vollen und dem ersten leeren Band auch vorhanden, aber etwas kleiner, so dass gerade die kurzwelligsten, energiereichsten Quanten ausreichen, Elektronen vom unteren in das obere Band zu heben, und daher absorbiert werden können, nicht aber die mittel- und langwelligen Photonen. Kurzwelliges (blauviolettes und blaues) Licht kann absorbiert werden und wird absorbiert, die Substanzen sind daher gelb. Beispiele dafür sind Schwefel, Kadmiumsulfid (CdS, als Pigment Kadmiumgelb, als Mineral Greenockit), Auripigment As₂S₃.


Schwefel	Kadmiumgelb hell, Kadmiumgelb mittel, Kadmiumorange (Aquarellfarben)

Bei noch geringerem Bandabstand können auch schon die Quanten des mittelwelligen Lichts absorbiert werden und nur die langwelligen (roten) nicht. Diese Substanzen sind rot, wie z.B Zinnober HgS, Realgar AsS. Ist die Bandlücke so klein, dass alles sichtbare Licht absorbiert werden kann, so ist die Substanz schwarz; ein Beispiel dafür ist Kadmiumselenid, CdSe.
Interessant ist, dass Kadmiumsulfid und Kadmiumselenid Mischkristalle bilden können. Je höher der Selenidanteil, desto kleiner wird die Bandlücke, und die Farbe verschiebt sich von Gelb über Orange nach Rot und schließlich Schwarz.
Im Gegensatz zu den durch Fremdatome gefärbten und im reinen Zustand farblosen Substanzen sind die hier behandelten Kristalle „stark“ farbig, die Farbe bleibt auch im pulverisiertem Zustand erhalten, die Strichfarbe der Mineralien entspricht ihrer Farbe. Dies qualifiziert diese Substanzen als Farbmittel, „Pigmente“.
Ist die Lücke schließlich so klein, dass der geringe Bandabstannd auch durch Wärmeenergie überwunden werden kann, so wird die Substanz zum Halbleiter. Graphit sei als Beispiel genannt. Verschwindet die Lücke zwischen den Bändern ganz, indem sich die Bänder überlappen, so hat die Substanz metallische Eigenschaften und das bekannte metallische Aussehen.

Glanz und Farbe der Metalle

Die elektrischen und auch die optischen Eigenschaften der Metalle kommen durch die Existenz der Leitungselektronen zustande, das sind die Elektronen innerhalb des nur teilweise besetzten Energiebandes, die weitgehend frei beweglich sind. Aus der Bandstruktur der Metalle kann man ablesen, dass ein Metall elektromagnetische Strahlung aller Frequenzen, von der Wärmestrahlung bis zum Ultraviolett absorbieren kann. Man könnte meinen, dass Metalle daher schwarz sein müssten.

Feinster Metallstaub ist schwarz, aber als Folge der elektrischen Leitfähigkeit reflektieren größere Metallstücke das Licht, die Metalle glänzen und erscheinen um so heller, je größer ihr Reflexionsvermögen ist.

Für die folgenden Überlegungen sind die Details der Bandstruktur ohne Bedeutung, als Modell für ein Metall kann man sich daher ein Elektronengas vorstellen, dessen Ladung durch die des unbeweglichen positiven Ionengitters ausgeglichen ist.
Die gute elektrische Leitfähigkeit hat zur Folge, dass elektrische Spannungen zwischer verschiedenen Punkten schnell abgebaut werden, indem elektrischer Strom fließt. Elektrische Felder bewirken Ladungstransport, und in einem idealen Leiter können überhaupt keine elektrischen Feldstärken auftreten, weil sie ohne Verzögerung ausgeglichen werden.
Lässt man nun eine elektromagnetische Welle auf einen idealen Leiter auftreffen, dann muss an der Oberfläche die elektrische Feldstärke Null sein. Auch dafür kann man ein mechanisches Modell zur Veranschaulichung heranziehen: Wenn man ein Ende eines Seiles fest einspannt, das Seil spannt und dann eine Welle losschickt, dann muss die Auslenkung an der festgehaltenen Stelle Null sein, und das führt dazu, dass die Welle reflektiert wird, wobei sich aber ihr Vorzeichen umkehrt.

◊

Eine Welle in einem elastischen gespannten Seil, die am festgehaltenen Ende reflektiert wird.

Man kann die Erfüllung der Randbedingung rechnerisch erreichen, indem man eine entgegengesetzt gleiche Welle, die in entgegengesetzter Richtung läuft, addiert. Bei der Reflexion am festen Ende kehrt sich die Richtung der Auslenkung um.

Je besser die Leitfähigkeit, desto vollständiger die Reflexion. Der Glanz der Metalle ist eine Folge ihrer elektrischen Leitfähigkeit!

Silber und Aluminium, beides sehr gute Leiter, reflektieren entsprechend vollständiger als beispielsweise das viel schlechter leitende Eisen: Für Licht der gelben Natriumlinie (589,3 nm) ist das Reflexionsvermögen der drei Metalle 94%, 83% und 33% (nach Born u. Wolf 1975)

Die Leitfähigkeit ist natürlich niemals unendlich, insbesondere steht bei höheren Frequenzen auch die Trägheit der Elektronen infolge ihrer Masse einem sofortigen Abbau der Feldstärke im Wege. Oberhalb einer bestimmten Frequenz macht sich die Trägheit der Ladungsträger immer mehr bemerkbar, und das Metall wird für zunehmende Frequenzen einem Isolator immer ähnlicher, d.h. es wird durchsichtiger, und sein Reflexionsvermögen lässt entsprechend nach.
Die charakteristische Frequenz, bei der der Übergang zur Transparenz erfolgt, ist umso höher, je größer die Dichte der Ladungsträger ist und je leichter diese sind. Mit einfachen Modellannahmen ergibt sich die Formel

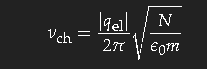
(q_el ist die Ladung, N die Dichte und m die Masse der Ladungsträger), die die Größenordnung richtig wiedergibt. Der exakte Wert hängt allerdings von feineren Details der Bandstruktur ab. Bei den meisten Metallen liegt die charakteristische Frequenz im Ultraviolett.
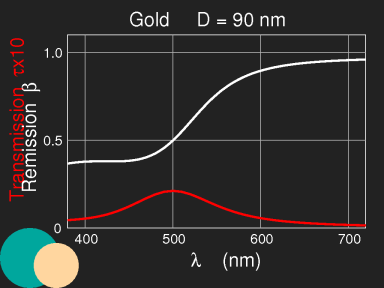
Bei Kupfer, Silber und Gold rührt die Farbe daher, dass langwelliges Licht besser reflektiert wird als kurzwelliges, das tiefer ins Material eindringt und dort absorbiert wird. Die charakteristischen Frequenzen von Kupfer und Gold liegen im optischen Bereich; an dünnen Goldfolien oder bedampften Gläsern kann man auch die Durchlässigkeit sehen; das hauchdünne Blattgold erscheint in der Durchsicht grünblau.

Ein Stück Blattgold (24 Karat), links bei normaler Beleuchtung, rechts von hinten durchleuchtet.

Remissions- und Transmissionskurven einer Goldfolie (experimentelle Daten: http://refractiveindex.info/) und links unten die daraus berechneten Farben für Transmission und Remission.

Gold ist mit Silber und mit Kupfer in jedem Verhältnis legierbar (mischbar). Reines Gold ist rötlichgelb; mit zunehmendem Silbergehalt wird es gelb, dann blass grünlichgelb, dann weiß (Weißgold); mit Kupfer legiert wird die Farbe immer rötlicher.

Bei Elektrolyten, z.B. einer Kochsalzlösung, liegt die charakteristische Frequen so niedrig, dass ihr optisches Verhalten dem von Isolatoren gleicht.

Metallische Nanopartikel

Ganz andere Farben treten auf, wenn die Metalle in Form von Partikeln vorliegen, deren Abmessungen klein gegen die Lichtwellenlängen sind. Goldrubinglas, das seine Farbe durch solche Goldpartikeln bekommt, ist das bekannteste Beispiel. Der Goldgehalt ist gering, nur etwa 0.01 bis 0.02 Gewichtsprozent. Das Gold wird der Glasschmelze in Form von Tetrachlorogold(III)-säure („Goldchlorid“), das man durch Auflösen von Gold in Königswasser erhält, zugesetzt. Nach dem raschen Abkühlen ist das goldhaltige Glas noch farblos transparent, nach neueren Untersuchungen liegt das Gold in diesem Stadium in Form von einwertigen Ionen vor (F.E. Wagner et al.). Durch Wärmebehandlung bei ca. 600º Celsius entsteht schließlich die gewünschte kolloidale Goldlösung im Glas, indem sich die Goldatome zu kleinen metallischen Aggregaten zusammenschließen.

Links vorne: Goldrubinglas in Überfangtechnik,
Mitte: Überfangkappen aus reinem Goldrubinglas, vor der Wärmebehandlung klar, nachher rubinrot,
hinten: Glas mit Färbung aus Silber-Nanopartikeln
(Hersteller: Nachtmann)
Foto: Deutsches Museum

Es ist nicht möglich, diese Farbe in einfachen Modellen anschaulich plausibel zu machen. Wie man sie berechnen kann, hat Gustav Mie im Jahr 1908 gezeigt: Lösung der elektromagnetischen Feldgleichungen (Maxwellgleichungen) unter Verwendung der experimentellen Daten für Brechungsindex und Absorptionskoeffizienten.

Farbe von Goldrubinglas, berechnet für kugelförmige Teilchen mit Radius 7 nm (experimentelle Daten wie oben: http://refractiveindex.info/). Die Skala unter dem Bild gibt die Schichtdicke, multipliziert mit der Teilchendichte und der Querschnittsfläche eines Teilchens an. Details der Berechnung im Abschnitt “Mie scattering”.

Die Lichtwellen regen Schwingungen der Elektronen im Metall an, diese werden durch den elektrischen Widerstand gedämpft – die Strahlung wird absorbiert, in Wärme umgewandelt. Die mikroskopische Dynamik wird durch den Brechungsindex und die Absorptionszahl phänomenologisch erfasst. Die Stärke der Absorption wurde bei der Behandlung der Farbstoffe abgeschätzt, dort haben wir gesehen, dass es auf die Größe der absorbierenden Moleküle oder Teilchen ankommt (solange diese klein im Vergleich zur Wellenlänge des Lichts sind). Die Nanopartikel sind viel größer als Farbstoffmoleküle und können daher Licht der entsprechenden Wellenlängen noch viel besser absorbieren.

Fehlstellen, Farbzentren

Ein weiterer Mechanismus kann zur Buntheit von im reinen Zustand farblosen Substanzen führen, nämlich falsche Besetzung einzelner Gitterplätze, wozu auch Fehlstellen, d.h. das Leerbleiben von Gitterplätzen, gerechnet werden soll.

Fluorit (Kristall-Spaltstücke). Fluorit, CaF₂, erhält seine Farbe vermutlich durch Fehlstellen. Diese können durch radioaktive Bestrahlung oder durch Verunreinigungen hervorgerufen sein.

Betrachten wir als einfachstes Beispiel eine Fehlstelle in einem Alkalihalogenidkristall. In dem Kristall sei ein schwacher Überschuss des Alkalimetalls vorhanden, d.h. es fehlen Halogenionen. Da der Kristall insgesamt elektrisch ungeladen ist, sind innerhalb des Gitters Elektronen vorhanden, und zwar zu jeder derartigen Fehlstelle eines. (Man könnte meinen, dass die überschüssigen Metallatome nicht ionisiert würden; aber ins Gitter eingebaut, unterscheiden sie sich nicht von den anderen, liegen daher gleichermaßen ionisiert vor.) Das überschüssige Elektron wird durch elektrische Kräfte in der Nähe des unbesetzten Gitterplatzes gehalten, es ergibt sich gleichsam ein gebundener Zustand mit dem unbesetzten Gitterplatz als Zentrum.
Und nun ist die Argumentation genau dieselbe wie bei der Begründung des Termschemas für ein einzelnes Atom (siehe „atomare Spektren“). Das Elektron wird durch eine Wellenfunktion beschrieben. Dadurch ergeben sich für das Teilchen wieder diskrete mögliche Energien; die Fehlstelle verhält sich wie ein quasi-atomares Gebilde innerhalb des Kristalls. Zwischen den Energiebändern werden durch die Fehlstellen neue Niveaus geschaffen und dadurch die Möglichkeiten der Absorption von Lichtquanten vergrößert. Die Anregungsenergie des an die Fehlstelle gebundenen Elektrons liegt im Bereich der Energien des sichtbaren Lichts, daher der Name „F-Zentrum“ (F wie Farbe).
Da sich fehlende Elektronen im Kristall auch wie Teilchen verhalten („Löcher“), ist die Situation auch bei Alkaliunterschuss ähnlich. Auch wenn in einem Kristallgitter statt eines vierwertigen Ions ein fünf- oder dreiwertiges, etwa gleich großes eingefügt ist, ergeben sich ähnliche Verhältnisse, eine Überschussladung an einem Gitterplatz und ein Elektron oder „Loch“ (Defektelektron), das sich in dessen Umgebung aufhält.
Benachbarte Fehlstellen können sich beeinflussen, es können sich quasimolekulare Strukturen innerhalb des Kristallgitters ausbilden, insbesondere auch zwischen verschiedenartigen Fehlstellen, z.B. Fremdatomen und Leerstellen. So ergibt sich eine Fülle von verschiedenen Möglichkeiten.

Lumineszenz (Fluoreszenz unf Phosphoreszenz)

Bei der Besprechung des Rubins wurde auch schon kurz auf dessen Fluoreszenz eingegangen. Die Übergänge zwischen verschiedenen Energiezuständen, die unter Absorption von Licht vonstatten gehen, können auch in umgekehrter Richtung ablaufen, wobei Lichtquanten emittiert werden. Wie beim Rubin schon gesagt, kann die Anregungsenergie aber auch durch konkurrierende Prozesse abgegeben werden – als unsichtbare Infrarotstrahlung oder durch Anregung von Gitterschwingungen (Wärmebewegung). In den meisten Fällen überwiegt daher die Absorption die Emission bei weitem. Wenn die Emission bei niedrigen Temperaturen sichtbar wird, spricht man von Lumineszenz. Diesen Erscheinungen ist ein eigener Abschnitt gewidmet.

Pigmente

Pigmente im Verkaufsregal. Von links nach rechts: Echtlichtgelb, Goldocker, Englischrot, Eisenoxidgelb, Terra di Siena natur, Chromoxid.

Stark farbige mineralische Substanzen eignen sich zur Verwendung als Farbmittel, Pigmente, wenn sie wasserunlöslich und hinreichend beständig gegen Witterungseinflüsse sind. Einige wurden als Beispiele vorgestellt, um die farbgebenden Mechanismen zu illustrieren.
Sie finden im Internet Angaben über die Herkunft und historische Entwicklung anorganischer Pigmente, Listen mit den gängigen Pigmenten, wie sie für Malerei und Herstellung von Farben verwendet werden, und Angaben über deren chemische Zusammensetzung. Zum Beispiel hier: Farbmittel und natürlich auch in der Wikipedia. Diesen Zusammenstellungen können Sie auch entnehmen, was sich hinter den Namen der im obigen Bild gezeigten Pigmente verbirgt, und Sie finden dort auch Angaben über die Ursachen der Farbigkeit.

Zurück zur Übersicht: Wie kommt Farbe zustande?

Kristalle, Mineralien, Metalle, Pigmente